题目内容
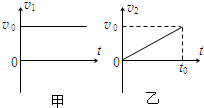
一小船欲渡过宽为d的河流,船头方向始终与河岸垂直,河水的流速v1随时间t的关系如图甲所示,小船在静水中的速度v2随时间t的关系如图乙所示.设小船从t=0时开始出发,t=t0时恰好到达河对岸,则下列说法正确的是( )
A.小船到达河对岸时的速度为
| ||
B.小船过河的平均速度为
| ||
C.小船到达河对岸时的位移为
| ||
D.小船到达河对岸时的路程为
|

A、船头方向始终与河岸垂直,则渡河最短时间为t0,小船在静水中做初速度为零的匀加速运动,当到达河岸时速度为静水中速度与水流速度的合成,即为
=
v0,故A正确;
B、小船在静水中做初速度为零的匀加速运动,水流速度不变,则小船过河的平均速度为
=
v0,故B错误;
C、由于沿河岸方向上的位移为:x=v0t0,所以小船到达河对岸时的位移
,故C错误;
D、由题意可在,小船做曲线运动,无法确定过河的路程,故D错误;
故选:A.
|
| 2 |
B、小船在静水中做初速度为零的匀加速运动,水流速度不变,则小船过河的平均速度为
(
|
| ||
| 2 |
C、由于沿河岸方向上的位移为:x=v0t0,所以小船到达河对岸时的位移
| d2+(v0t)2 |
D、由题意可在,小船做曲线运动,无法确定过河的路程,故D错误;
故选:A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

