题目内容
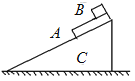
【题目】竖直平面内光滑的半圆形轨道和水平轨道相切与B点，质量
的滑块甲从A点以初速度
沿水平面向左滑行，与静止在B点
的滑块乙碰撞且碰撞过程没有能量损失。碰撞后滑块乙恰好通过C点。已知半圆形轨道半径
，两滑块与水平轨道的动摩擦因数均为
（g=10 m/s2）
（1）A点到B点的距离
；
（2）假设滑块乙与地面碰撞后不弹起，求两滑块静止时的距离。
【答案】（1）
（2）
【解析】（1）滑块甲从A点到B点，根据动能定理有： 
甲与乙碰撞过程为弹性碰撞，有： 
解得
， 
滑块乙恰好通过最高点C，则有
从B点到C点，根据功能关系则有
，整理可得
（2）滑块甲碰后反向向右匀减速运动直到停止，滑行距离根据动能定理有： 
，解得
滑块乙从C点离开轨道做平抛运动，水平位移
滑块乙落地时与地面碰撞，水平方向动量守恒，则可得落地后速度
若乙继续向右滑行距离
，则有
，解得
所以最终滑块甲乙的距离为
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
