��Ŀ����
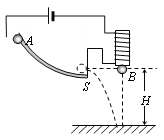
����Ŀ����ͼ��ʾ��һ����ΪM�ij�ľ�徲ֹ��ˮƽ���ϣ���һ����Ϊm��С������һ����ˮƽ�ٶȳ���ľ�壬��֪�����ľ��֮��Ķ�Ħ������Ϊ![]() �����Ħ�������ڻ���Ħ��������
�����Ħ�������ڻ���Ħ��������

��1����������ľ���ϻ���ʱ��ľ���ܱ��־�ֹ������ľ��͵���֮��Ķ�Ħ������������ʲô������
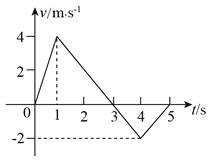
��2������ľ�������M=0��2kg����ľ����ˮƽ���Ķ�Ħ��������=0��1�����������ҲΪ0��2kg��������v0=1��2m/s���ٶȻ��ϳ������ˣ�С�����볤ľ���Ķ�Ħ��������0=0��4����������û�л��볤ľ�壬���ڿ�ʼ���ϳ�ľ�嵽���ֹ�����Ĺ����У����黬�еľ����Ƕ��٣���g=10m/s2��
���𰸡���1��![]() ����2��
����2��![]()
�������������������1������Գ�ľ���Ħ����ˮƽ���ң�![]()
����Գ�ľ���Ħ����ˮƽ�������Ħ����![]()
��ʹľ���ܱ��־�ֹ������������![]()
��ã�![]()
��2�����黬��ľ�壬���Ҽ��٣�ľ�����Ҽ��٣�ֱ�������й�ͬ�ٶȣ��˺����Թ�ͬ�ļ��ٶ����Ҽ��١�
����ţ�ٵڶ����ɣ��Ի��飬�У�![]() ��������ٵļ��ٶ�
��������ٵļ��ٶ�![]()
��ľ�壬�У�![]() ��ľ����ٵļ��ٶ�
��ľ����ٵļ��ٶ�![]()
��![]() ��֪���ӿ�ʼ�˶�������ͬ������ʱ��
��֪���ӿ�ʼ�˶�������ͬ������ʱ��![]() ����ͬ�ٶ�
����ͬ�ٶ�![]()
������Ծ�ֹǰ������λ��![]()
�����й�ͬ�ٶȺ�����һ����٣�����ţ�ٵڶ����ɣ���![]()
��ã�![]() ���ʶ���ͬ�ٺ�һ�����Ҽ��٣�ֱ����ֹ��
���ʶ���ͬ�ٺ�һ�����Ҽ��٣�ֱ����ֹ��
��![]() ���ɵö���һ����ٵ�λ��
���ɵö���һ����ٵ�λ��![]()
�ʻ������λ��![]()

 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�