题目内容
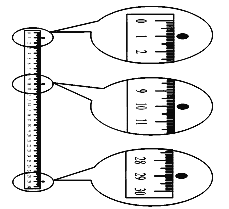
【题目】如图甲、乙、丙所示,三个完全相同的半圆形光滑绝缘轨道置于竖直平面内,左右两端点等高,其中图乙轨道处在垂直纸面向外的匀强磁场中,图丙轨道处在竖直向下的匀强电场中,三个相同的带正电小球同时从轨道左端最高点处由静止释放.则三个带电小球通过圆轨道最低点时( )
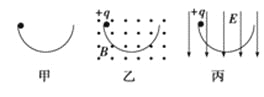
A. 速度相同
B. 所用时间相同
C. 对轨道的压力相同
D. 均能到达轨道右端最高点处
【答案】D
【解析】试题分析:在乙图中,因为洛仑兹力总是垂直于速度方向,故洛仑兹力不做功;滑块下落时只有重力做功,故甲和乙两次机械能均守恒,故两次滑块到最低点的速度相等, ![]() mv12=mgR,丙图中,小球下滑的过程中电场力做正功,重力做正功,
mv12=mgR,丙图中,小球下滑的过程中电场力做正功,重力做正功, ![]() mv22=mgR+qER,所以小球在最低点的速度等于甲图和乙图中的速度.故A错误;甲图和丙图比较可得,丙图中,小球的加速度比较大,所以达到最低点的时间要短.故B错误;小球在最低点时,甲图中重力和支持力提供向心力,而乙图中是重力、支持力和洛伦兹力提供向心力,所以小球受到的支持力大小不相等,对轨道的压力也不相等.故C错误;三个小球的运动过程中,重力做功,动能和重力势能之间转换;洛伦兹力不做功;电场力做功,电势能与动能之间转换;由于没有其他的能量损失,所以三种情况下,小球均能到达轨道右端最高点处,故D正确;故选D.
mv22=mgR+qER,所以小球在最低点的速度等于甲图和乙图中的速度.故A错误;甲图和丙图比较可得,丙图中,小球的加速度比较大,所以达到最低点的时间要短.故B错误;小球在最低点时,甲图中重力和支持力提供向心力,而乙图中是重力、支持力和洛伦兹力提供向心力,所以小球受到的支持力大小不相等,对轨道的压力也不相等.故C错误;三个小球的运动过程中,重力做功,动能和重力势能之间转换;洛伦兹力不做功;电场力做功,电势能与动能之间转换;由于没有其他的能量损失,所以三种情况下,小球均能到达轨道右端最高点处,故D正确;故选D.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目