题目内容
如图所示,定滑轮的半径r=2 cm,绕在滑轮上的细线悬挂着一个重物,由静止开始释放,测得重物以加速度a=2 m/s2做匀加速运动,在重物由静止下落距离为1 m的瞬间,滑轮边缘上的点的角速度ω=________rad/s,向心加速度a=________m/s2.

答案:100,200
解析:
提示:
解析:
|
重物下落1 m时,瞬时速度为 v= 显然,滑轮边缘上每一点的线速度也都是2 m/s,故滑轮转动的角速度,即滑轮边缘上每一点的转动角速度为ω= 向心加速度为a=ω2r=1002×0.02 m/s2=200 m/s2. |
提示:
|
本题讨论的是变速运动问题,重物落下的过程中滑轮运动的角速度、轮上各点的线速度都在不断增大,但在任何时刻角速度与线速度的关系(v=ωr),向心加速度与角速度、线速度的关系(a=ω2r=v2/r)仍然成立. |

练习册系列答案
相关题目
 如图所示,光滑的半球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,轻绳的一端系一小球.靠放在半球上的A点,另一端绕过定滑轮后用力拉住,使小球静止.现缓慢地拉绳,在使小球沿球面由A到半球的顶点B的过程中,半球对小球的支持力N和绳对小球的拉力T的大小变化情况是( )
如图所示,光滑的半球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,轻绳的一端系一小球.靠放在半球上的A点,另一端绕过定滑轮后用力拉住,使小球静止.现缓慢地拉绳,在使小球沿球面由A到半球的顶点B的过程中,半球对小球的支持力N和绳对小球的拉力T的大小变化情况是( )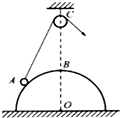 如图所示,光滑的半球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,轻绳的一端系一小球,靠在半球上的A点,另一端绕过定滑轮后用力拉住,使小球静止.现缓慢地拉绳,在使小球沿球面由A移动到半球的顶点B的过程中,半球对小球的支持力N和绳对小球的拉力T的变化情况是( )
如图所示,光滑的半球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,轻绳的一端系一小球,靠在半球上的A点,另一端绕过定滑轮后用力拉住,使小球静止.现缓慢地拉绳,在使小球沿球面由A移动到半球的顶点B的过程中,半球对小球的支持力N和绳对小球的拉力T的变化情况是( )

