Question

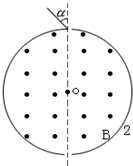
（2007?苍山县模拟）如图是某离子速度选择器的原理示意图，在一半径为R=10cm的圆柱形桶内有B=10^-4T的匀强磁场，方向平行于轴线，在圆柱桶某一直径两端开有小孔，作为入射孔和出射孔．离子束以不同角度入射，最后有不同速度的离子束射出．现有一离子源发射质荷比为

q

m

=2×10¹¹C/kg的阳离子，且离子束中速度分布连续．当角θ=45°，出射离子速度υ的大小是（　　）

• A．

  2

  ×106m/s
• B．2

  2

  ×106m/s
• C．2

  2

  ×108m/s
• D．4

  2

  ×106m/s

Answer 1

分析：离子束不经碰撞而直接从出身孔射出，即可根据几何知识画出轨迹，由几何关系求出轨迹的半径，即可由牛顿第二定律求速度v

解答：解：离子从小孔a射入磁场，与ab方向的夹角为α=45°，则离子从小孔b离开磁场时速度与ab的夹角也为α=45°，过入射速度和出射速度方向作垂线，得到轨迹的圆心O′，画出轨迹如图，由几何知识得到轨迹所对应的圆心角θ=2α=90°，则离子的轨迹半径

2

r=2R，r=

2

R=

2

×0.1m=

2

10

m
由牛顿第二定律得：
  qvB=

mv2

r

得：v=

qBr

m

=

q

m

?rB=2×10¹¹×

2

10

×10^-4=2

2

×10⁶m/s
故选：B

点评：本题的解题关键是根据几何知识画出离子的运动轨迹，得到半径，即可求解速度v．