题目内容
如图所示,一竖直平面内光滑圆形轨道半径为R,小球以速度v0经过最低点B沿轨道上滑,并恰能通过轨道最高点A。以下说法正确的是( )

A.v0应等于 ,小球到A点时速度为零
,小球到A点时速度为零
B.v0应等于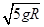 ,小球到A点时速度和加速度都不为零
,小球到A点时速度和加速度都不为零
C.小球在B点时加速度最大,在A点时加速度最小
D.小球从B点到A点,其速度的增量为(1+ )
)
【答案】
BCD
【解析】
试题分析:由于小球恰好能通过轨道的最高点,在最高点A处,根据牛顿第二定律有:mg=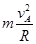 =maA,解得:vA=
=maA,解得:vA=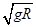 ,aA=g,故选项A错误;在由最低点到最高点的过程中,根据机械能守恒定律有:2mgR=
,aA=g,故选项A错误;在由最低点到最高点的过程中,根据机械能守恒定律有:2mgR= -
- ,解得:v0=
,解得:v0=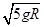 ,故选项B正确;小球在B点是重力势能最小,动能最大,在A点时重力势能最大,动能最小,因此在B点时加速度最大,在A点时加速度最小,故选项C正确;小球通过A、B两点时速度方向相反,因此在由B到A的过程中,其速度的增量为:Δv=vA-(-v0)=
,故选项B正确;小球在B点是重力势能最小,动能最大,在A点时重力势能最大,动能最小,因此在B点时加速度最大,在A点时加速度最小,故选项C正确;小球通过A、B两点时速度方向相反,因此在由B到A的过程中,其速度的增量为:Δv=vA-(-v0)=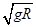 +
+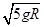 =(1+
=(1+ )
)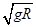 ,故选项D正确。
,故选项D正确。
考点:本题主要考查了圆周运动向心力公式、牛顿第二定律、机械能守恒定律的应用,以及矢量运算等问题,属于中档题。

练习册系列答案
相关题目
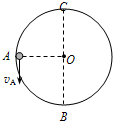 如图所示为一竖直平面内的光滑圆轨道,O是其圆心,A是轨道上与圆心等高的点,B是最低点,C是最高点,圆的半径为0.4m.有一个质量m=1kg的小球在此圆轨道的内侧运动,小球经过A点时的速率为
如图所示为一竖直平面内的光滑圆轨道,O是其圆心,A是轨道上与圆心等高的点,B是最低点,C是最高点,圆的半径为0.4m.有一个质量m=1kg的小球在此圆轨道的内侧运动,小球经过A点时的速率为 如图所示,一竖直平面内光滑圆形轨道半径为R,小球以速度v0经过最低点B沿轨道上滑,并恰能通过轨道最高点A.以下说法正确的是( )
如图所示,一竖直平面内光滑圆形轨道半径为R,小球以速度v0经过最低点B沿轨道上滑,并恰能通过轨道最高点A.以下说法正确的是( )
 ,小球到A点时速度为零
,小球到A点时速度为零 ,小球到A点时速度和加速度都不为零
,小球到A点时速度和加速度都不为零

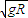 ,小球到A点时速度为零
,小球到A点时速度为零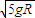 ,小球到A点时速度和加速度都不为零
,小球到A点时速度和加速度都不为零