题目内容
 如图所示,一竖直平面内光滑圆形轨道半径为R,小球以速度v0经过最低点B沿轨道上滑,并恰能通过轨道最高点A.以下说法正确的是( )
如图所示,一竖直平面内光滑圆形轨道半径为R,小球以速度v0经过最低点B沿轨道上滑,并恰能通过轨道最高点A.以下说法正确的是( )分析:小球恰好能通过最高点,可以先求出最高点速度vA,小球从最高点运动到最低点的过程中只有重力做功,机械能守恒,根据机械能守恒定律,可以进一步小球在B点的速度,还能得出小球从B点到A点过程中的速度增量,根据向心加速度公式,可以判断向心加速度的大小.
解答:解:小球恰好能通过最高点,根据牛顿第二定律
mg=m
解得
vA=
;
小球从最高点运动到最低点的过程中只有重力做功,机械能守恒
mg(2R)=
mv02-
mvA2
解得
v0=
;
根据向心加速度公式a=
,可知速度越大,向心加速度越大;
由于小球在最高点和最低点的速度反向,因而从最高点到最低点过程中速度的增量为(1+
)
;
故选BCD.
mg=m
| ||
| R |
解得
vA=
| gR |
小球从最高点运动到最低点的过程中只有重力做功,机械能守恒
mg(2R)=
| 1 |
| 2 |
| 1 |
| 2 |
解得
v0=
| 5gR |
根据向心加速度公式a=
| v2 |
| R |
由于小球在最高点和最低点的速度反向,因而从最高点到最低点过程中速度的增量为(1+
| 5 |
| gR |
故选BCD.
点评:本题关键抓住物体恰能通过最高点的临界条件,然后根据机械能守恒定律求出最低点速度,从而可以求从最高点到最低点过程中速度的增量,并判断各点的向心加速度大小.

练习册系列答案
相关题目
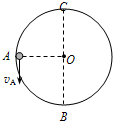 如图所示为一竖直平面内的光滑圆轨道,O是其圆心,A是轨道上与圆心等高的点,B是最低点,C是最高点,圆的半径为0.4m.有一个质量m=1kg的小球在此圆轨道的内侧运动,小球经过A点时的速率为
如图所示为一竖直平面内的光滑圆轨道,O是其圆心,A是轨道上与圆心等高的点,B是最低点,C是最高点,圆的半径为0.4m.有一个质量m=1kg的小球在此圆轨道的内侧运动,小球经过A点时的速率为
 ,小球到A点时速度为零
,小球到A点时速度为零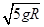 ,小球到A点时速度和加速度都不为零
,小球到A点时速度和加速度都不为零 )
)

 ,小球到A点时速度为零
,小球到A点时速度为零 ,小球到A点时速度和加速度都不为零
,小球到A点时速度和加速度都不为零

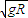 ,小球到A点时速度为零
,小球到A点时速度为零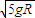 ,小球到A点时速度和加速度都不为零
,小球到A点时速度和加速度都不为零