题目内容
7.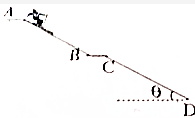 如图所示为一滑雪跳台,滑雪运动员从A点由静止开始下滑至C点飞出,设从A至C运动员只滑行,BC段水平,CD段与水平面成θ角,tanθ=$\frac{3}{4}$,A、B的竖直高度差是40m,雪面和空气阻力忽略不计,求滑雪运动员落在CD段上的位置.
如图所示为一滑雪跳台,滑雪运动员从A点由静止开始下滑至C点飞出,设从A至C运动员只滑行,BC段水平,CD段与水平面成θ角,tanθ=$\frac{3}{4}$,A、B的竖直高度差是40m,雪面和空气阻力忽略不计,求滑雪运动员落在CD段上的位置.
分析 应用动能定理求出运动员离开C点的速度,运动员离开C点后做平抛运动,应用平抛运动的运动规律可以求出运动员落地位置.
解答 解:雪面和空气阻力忽略不计,则整个过程中只有重力做功,
运动员从A到C过程,由动能定理得:mgh=$\frac{1}{2}$mvC2-0,
解得:vC=$\sqrt{2gh}$=$\sqrt{2×10×40}$=20$\sqrt{2}$m/s,
离开C点后运动员做平抛运动,
tanθ=$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{C}t}$=$\frac{gt}{2{v}_{C}}$=$\frac{3}{4}$,
解得:t=$\frac{3{v}_{C}}{2g}$=$\frac{3×20\sqrt{2}}{2×10}$=3$\sqrt{2}$s,
运动员的水平位移:
x=vCt=20$\sqrt{2}$×3$\sqrt{2}$=120m,
已知:tanθ=$\frac{3}{4}$,则cosθ=$\frac{4}{5}$,
运动员的位移大小:s=$\frac{x}{cosθ}$=$\frac{120}{\frac{4}{5}}$=150m,
则运动员落地点到C点的距离为150m.
答:滑雪运动员落在CD段距C点的距离为150m处.
点评 本题考查了求运动员的落点位置,分析清楚运动员的运动过程,应用动能定理、平抛运动规律即可正确解题,解题时注意数学知识的应用.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
17.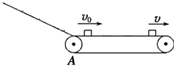 在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )
在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )
 在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )
在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )| A. | 工件滑上传送带到与传送带相对静止所需时间为$\frac{v-{v}_{0}}{g}$ | |
| B. | 因传送工件电动机多做的功为$\frac{1}{2}$m(v2-v02) | |
| C. | 传送带的摩擦力对工件所做的功为$\frac{1}{2}$m(v-v0)2 | |
| D. | 工件与传送带的相对位移为$\frac{(v-{v}_{0})^{2}}{2μg}$ |
18.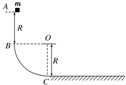 如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )
如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )
 如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )
如图所示,BC是竖直面内的四分之一圆弧形光滑轨道,下端C与水平直轨道相切.一个小物块从B点正上方R处的A点处由静止释放,从B点刚好进入圆弧形光滑轨道下滑,已知圆弧形轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因数μ=0.5,取g=10m/s2.小物块在水平面上滑动的最大距离是( )| A. | 0.1m | B. | 0.2m | C. | 0.6m | D. | 0.8m |
15.如图所示,帆板在海面上以速度v朝正西方向运动,帆船以速度v朝正北方向航行,以帆板为参照物( )
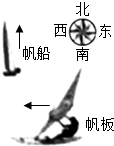

| A. | 帆船朝正东方向航行,速度大小为v | |
| B. | 帆船朝正西方向航行,速度大小为v | |
| C. | 帆船朝南偏东45°方向航行,速度大小为$\sqrt{2}$v | |
| D. | 帆船朝北偏东45°方向航行,速度大小为$\sqrt{2}$v |
12.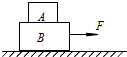 如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右匀速运动,设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.若水平外力F突然增大,但A、B仍保持相对静止,设此时A、B之间的摩擦力为f3,B与水平桌面间的摩擦力为f4,则( )
如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右匀速运动,设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.若水平外力F突然增大,但A、B仍保持相对静止,设此时A、B之间的摩擦力为f3,B与水平桌面间的摩擦力为f4,则( )
 如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右匀速运动,设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.若水平外力F突然增大,但A、B仍保持相对静止,设此时A、B之间的摩擦力为f3,B与水平桌面间的摩擦力为f4,则( )
如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右匀速运动,设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.若水平外力F突然增大,但A、B仍保持相对静止,设此时A、B之间的摩擦力为f3,B与水平桌面间的摩擦力为f4,则( )| A. | f1=f3 | B. | f1<f3 | C. | f2=f4 | D. | f2<f4 |
19.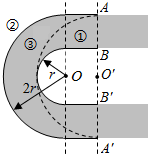 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )| A. | 选择路线①,赛车经过的路程最短 | |
| B. | 选择路线②,赛车的速率最小 | |
| C. | 选择路线③,赛车所用时间最短 | |
| D. | ①、②、③三条路线的圆弧上,赛车的向心加速度大小相等 |
16.一带正电的小球向右水平抛入范围足够大的匀强电场,电场方向水平向左,不计空气阻力,则小球( )
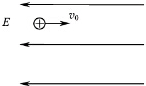

| A. | 做直线运动 | B. | 做曲线运动 | ||
| C. | 速率先减小后增大 | D. | 速率先增大后减小 |
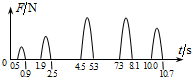 为了测量蹦床运动员从蹦床上跃起的高度,探究小组设计了如下的方法:在蹦床的弹性网上安装压力传感器,利用传感器记录运动员在运动过程中对弹性网的压力,来推测运动员跃起的高度.图为某段时间内蹦床的压力-时间图象.不计空气阻力,运动员仅在竖直方向上运动,且可视为质点,则可估算出运动员在这段时间内跃起的最大高度为(g取10m/s2)( )
为了测量蹦床运动员从蹦床上跃起的高度,探究小组设计了如下的方法:在蹦床的弹性网上安装压力传感器,利用传感器记录运动员在运动过程中对弹性网的压力,来推测运动员跃起的高度.图为某段时间内蹦床的压力-时间图象.不计空气阻力,运动员仅在竖直方向上运动,且可视为质点,则可估算出运动员在这段时间内跃起的最大高度为(g取10m/s2)( )