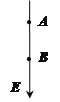题目内容
【题目】如图,A、B两球(可视为质点)质量均为m,固定在轻弹簧的两端,分别用细绳悬于O点,其中球A处在光滑竖直墙面和光滑水平地面的交界处。已知两球均处于静止状态,OA沿竖直方向,OAB恰好构成一个正三角形,重力加速度为g,则下列说法正确的是
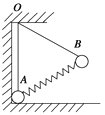
A. 球A对竖直墙壁的压力大小为![]()
B. 弹簧对球A的弹力大于对球B的弹力
C. 绳OB的拉力大小等于mg
D. 球A对地面的压力不可能为零
【答案】C
【解析】试题分析:C、对B球受力分析,受重力、支持力和拉力,如图;
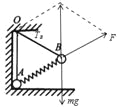
由于三个力夹角均为120°,故弹簧的支持力和绳子OB的拉力都等于重力mg,故C正确;A、对A球受力分析,受重力、弹簧的压力,墙壁的向右的支持力、细线的拉力、地面的支持力,(其中地面的支持力和拉力可能只有一个),在水平方向:![]() ,故A错误;B、弹簧静止,合力为零,故两个球对弹簧的弹力等大、反向、共线,故弹簧对球A的弹力等于对球B的弹力,故B错误;D、根据平衡条件,绳OA对球A的拉力和地面的支持力的合力大小等于弹簧推力的竖直分力和重力之和,故N+T=mg+Fsin30°,故T≤1.5mg,0≤N≤1.5mg.可知地面对A的支持力可能等于0,根据牛顿第三定律,球A对地面的压力可能为零.故D错误;故选C.
,故A错误;B、弹簧静止,合力为零,故两个球对弹簧的弹力等大、反向、共线,故弹簧对球A的弹力等于对球B的弹力,故B错误;D、根据平衡条件,绳OA对球A的拉力和地面的支持力的合力大小等于弹簧推力的竖直分力和重力之和,故N+T=mg+Fsin30°,故T≤1.5mg,0≤N≤1.5mg.可知地面对A的支持力可能等于0,根据牛顿第三定律,球A对地面的压力可能为零.故D错误;故选C.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目