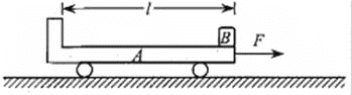
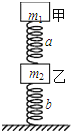
题目内容
【题目】如图所示,BC为半径R=0.8m的四分之一圆弧固定在水平地面上,AB为水平轨道,两轨道在B处相切连接。AB轨道上的滑块P通过不可伸长的轻绳与套在竖直光滑细杆的滑块Q连接。P、Q均可视为质点且圆弧轨道C点与竖直杆间距离足够远,开始时,P在A处,Q在与A同一水平面上的E处,且绳子刚好伸直处于水平,固定的小滑轮在D处,DE=0.35m,现把Q从静止释放,当下落h=0.35m时,P恰好到达圆弧轨道的B点,且刚好对B无压力,并且此时绳子突然断开,取g=10m/s2。求:
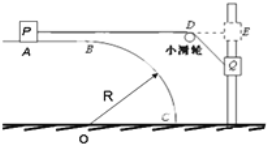
(1)在P到达B处时,P、Q的速度大小分别为多少(结果可保留根式);
(2)滑块P、Q落地的时间差。
【答案】(1)![]() ;
;![]() (2)0.3s
(2)0.3s
【解析】
试题分析:(1)P恰好到达圆弧轨道的B,且对B无压力,重力提供向心力,根据向心力公式得:
![]()
解得:![]()
P到达B点时,绳子的速度等于P的速度,根据几何关系知绳与竖直方向夹角为45°,

(2)绳子断后,P做平抛运动 ![]() ①
①
Q做竖直下抛运动R﹣h=vQt![]() ②
②
△t=t1﹣t2 ③
由①②③得△t=0.3s

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目