题目内容
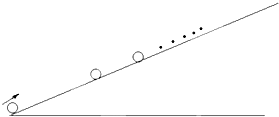
在足够长的斜面底端,每隔0.2s沿斜面向上抛出一个小球,小球初速度都为6m/s,已知小球匀减速上升和返回过程的加速度都为沿斜面向下的5m/s2.设各小球在运动中都不相碰.如图所示.求
(1)小球减速上升的时间和沿斜面上滑的最大位移
(2)第一个小球在抛出点以上能遇到的小球个数附加问(本问不计入总分)
(3)较长时间后,每一个小球与多少个小球在抛出点上方相遇.

解:(1)以初速度方向为正方向,根据题意,设小球上升时间为t,位移为s
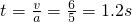
由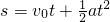 得:
得: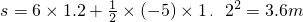
(2)经分析,物体返回时间也为1.2s;
在2.4s时,第13个小球恰抛出,则第一个小球在抛出点上方,会与11个小球相遇;
(3)第23个球上升过程时会与前面的第2-第22个球在上升阶段相遇,即与21个球相遇;
下降阶段相遇球的数量与第二问相等,为11个;
故共与21+11=32个小球相遇;
答:(1)小球减速上升的时间为1.2s,沿斜面上滑的最大位移为3.6m;
(2)第一个小球在抛出点以上能遇到的小球个数为11个;
(3)较长时间后,每一个小球与32个小球在抛出点上方相遇.
分析:(1)根据速度时间关系公式列式求解时间,根据位移时间关系公式列式求解位移;
(2)计算出小球返回的时间,在这段时间内上抛和之前上抛的小球都会与第一个小球相遇;
(3)第23个球上升过程时会与前面的第2-第22个球在上升阶段相遇,下降阶段相遇球的数量与第二问相等.
点评:本题后两位问的特点是小球个数多,可以给小球编号后画出草图和临界状况图分析,难题.
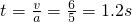
由
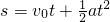 得:
得: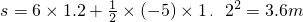
(2)经分析,物体返回时间也为1.2s;
在2.4s时,第13个小球恰抛出,则第一个小球在抛出点上方,会与11个小球相遇;
(3)第23个球上升过程时会与前面的第2-第22个球在上升阶段相遇,即与21个球相遇;
下降阶段相遇球的数量与第二问相等,为11个;
故共与21+11=32个小球相遇;
答:(1)小球减速上升的时间为1.2s,沿斜面上滑的最大位移为3.6m;
(2)第一个小球在抛出点以上能遇到的小球个数为11个;
(3)较长时间后,每一个小球与32个小球在抛出点上方相遇.
分析:(1)根据速度时间关系公式列式求解时间,根据位移时间关系公式列式求解位移;
(2)计算出小球返回的时间,在这段时间内上抛和之前上抛的小球都会与第一个小球相遇;
(3)第23个球上升过程时会与前面的第2-第22个球在上升阶段相遇,下降阶段相遇球的数量与第二问相等.
点评:本题后两位问的特点是小球个数多,可以给小球编号后画出草图和临界状况图分析,难题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目

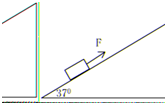 如图示,在倾角为37°的足够长的斜面底端有一质量为m=1.0kg的物体,现用绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行与斜面向上,物体以2m/s2向上匀加速运动.经时间t1=4秒时绳子断了.(sin37°=0.6 cos37°=0.8 g=10m/s2)求:
如图示,在倾角为37°的足够长的斜面底端有一质量为m=1.0kg的物体,现用绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行与斜面向上,物体以2m/s2向上匀加速运动.经时间t1=4秒时绳子断了.(sin37°=0.6 cos37°=0.8 g=10m/s2)求: