题目内容
 如图所示,通电导体棒ab质量为m、长为L,水平地放置在倾角为θ的光滑斜面上,通以图示方向的电流,电流强度为I,要求导体棒ab静止在斜面上.求:
如图所示,通电导体棒ab质量为m、长为L,水平地放置在倾角为θ的光滑斜面上,通以图示方向的电流,电流强度为I,要求导体棒ab静止在斜面上.求:(1)若磁场方向竖直向上,则磁感应强度B为多大?
(2)若要求磁感应强度最小,则磁感应强度的大小方向如何?
分析:(1)将立体图转换为平面图,对导线进行受力分析,根据共点力力平衡求出安培力的大小,从而根据F=BIL求出磁感应强度的大小.
(2)导线所受重力恒定,支持力的方向不变,根据三角形定则求出安培力的最小值,从而得出磁感应强度的最小值.
(2)导线所受重力恒定,支持力的方向不变,根据三角形定则求出安培力的最小值,从而得出磁感应强度的最小值.
解答: 解:(1)若磁场方向竖直向上,从a向b观察,导线受力情况如图甲所示.
解:(1)若磁场方向竖直向上,从a向b观察,导线受力情况如图甲所示.
由平衡条件得:
在水平方向上:F-FNsinθ=0
在竖直方向上:mg-FNcosθ=0
其中F=BIL,联立以上各式可解得:
B=
.
(2)若要求磁感应强度最小,则一方面应使磁场方向与通电导线垂直,另一方面应调整磁场方向使与重力、支持力合力相平衡的安培力最小.
如图乙所示,由力的矢量三角形讨论可知,当安培力方向与支持力垂直时,安培力最小,对应磁感应强度最小,设其值为Bmin,则:
BminIL=mgsinθ,
得:Bmin=
根据左手定则判定知,该磁场方向垂直于斜面向上.
答:(1)若磁场方向竖直向上,则磁感应强度B为
.
(2)若要求磁感应强度最小,磁感应强度的最小值为
.方向垂直于斜面向上.
 解:(1)若磁场方向竖直向上,从a向b观察,导线受力情况如图甲所示.
解:(1)若磁场方向竖直向上,从a向b观察,导线受力情况如图甲所示.由平衡条件得:
在水平方向上:F-FNsinθ=0
在竖直方向上:mg-FNcosθ=0
其中F=BIL,联立以上各式可解得:
B=
| mgtanθ |
| IL |
(2)若要求磁感应强度最小,则一方面应使磁场方向与通电导线垂直,另一方面应调整磁场方向使与重力、支持力合力相平衡的安培力最小.
如图乙所示,由力的矢量三角形讨论可知,当安培力方向与支持力垂直时,安培力最小,对应磁感应强度最小,设其值为Bmin,则:
BminIL=mgsinθ,
得:Bmin=
| mgsinθ |
| IL |
根据左手定则判定知,该磁场方向垂直于斜面向上.
答:(1)若磁场方向竖直向上,则磁感应强度B为
| mgtanθ |
| IL |
(2)若要求磁感应强度最小,磁感应强度的最小值为
| mgsinθ |
| IL |
点评:解决本题的关键将立体图转换为平面图,运用共点力平衡求解力,以及会运用三角形定则求解力的最小值.

练习册系列答案
相关题目
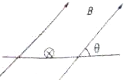 如图所示,通电导体棒静止于水平导轨上,棒的质量为m,长为L,通过的电流大小为I且垂直纸面向里,匀强磁场的磁感强度B的方向与导轨平面成θ角,则导体棒受到的( )
如图所示,通电导体棒静止于水平导轨上,棒的质量为m,长为L,通过的电流大小为I且垂直纸面向里,匀强磁场的磁感强度B的方向与导轨平面成θ角,则导体棒受到的( )| A、安培力大小为BIL | B、安培力大小为BILsinθ | C、摩擦力大小为BILsinθ | D、支持力大小为mg-BILcosθ |
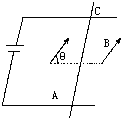 如图所示,通电导体棒AC静止于水平导轨上,棒的质量为m长为l,通过的电流强度为I,匀强磁场的磁感强度B的方向与导轨平面成θ角,求导轨受到AC棒的压力和摩擦力各为多大?
如图所示,通电导体棒AC静止于水平导轨上,棒的质量为m长为l,通过的电流强度为I,匀强磁场的磁感强度B的方向与导轨平面成θ角,求导轨受到AC棒的压力和摩擦力各为多大?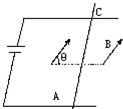 如图所示,通电导体棒AC静止于水平导轨上,棒的质量为m长为l,通过的电流强度为I,匀强磁场的磁感应强度B的方向与导轨平面成θ角.
如图所示,通电导体棒AC静止于水平导轨上,棒的质量为m长为l,通过的电流强度为I,匀强磁场的磁感应强度B的方向与导轨平面成θ角.