题目内容
1．某体积可变的贮气筒的现氢气体积为100L，贮有温度为27℃，压强为20大气压的氢气，后温度升高为127℃，压强升高为30个大气压，求现在氢气体积？分析 知道气体变化前的压强、体积和温度，还有变化后的压强和温度，根据理想气体状态方程即可计算体积的大小．
解答 解：氢气原来的状态为P1=20atm，V1=100L，T1=300K，
变化后的状态为P2=30atm，V2=？，T2=400K，
根据理想气体状态方程可得，
$\frac{{P}_{1}{V}_{1}}{{T}_{1}}=\frac{{P}_{2}{V}_{2}}{{T}_{2}}$
即$\frac{20atm×100L}{300K}=\frac{30atm×{V}_{2}}{400K}$
解得：V2=$\frac{800}{9}$L，
答：氢气体积为$\frac{800}{9}$L．
点评 本题是理想气体状态方程的直接的应用，分析清楚气体变化前后的状态直接计算即可，比较多简单．
练习册系列答案
相关题目
2．
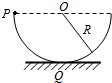如图，一半径为R的半圆形轨道竖直固定放置，轨道两端等高；质量为m的质点自轨道端点P由静止开始滑下，滑到最低点Q时，对轨道的正压力为2mg，重力加速度大小为g．质点自P滑到Q的过程中，克服摩擦力所做的功为（ ）
如图，一半径为R的半圆形轨道竖直固定放置，轨道两端等高；质量为m的质点自轨道端点P由静止开始滑下，滑到最低点Q时，对轨道的正压力为2mg，重力加速度大小为g．质点自P滑到Q的过程中，克服摩擦力所做的功为（ ）| A． | $\frac{1}{4}$mgR | B． | $\frac{1}{3}$mgR | C． | $\frac{1}{2}$mgR | D． | $\frac{π}{4}$mgR |
20．
如图所示，轻质弹簧一端固定，另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连，弹簧水平且处于原长，圆环从A处由静止开始下滑，经过B处的速度最大，到达C处的速度为零，AC=h，圆环在C处获得一竖直向上的速度v，恰好能回到A，弹簧始终在弹性限度内，重力加速度为g，则圆环（ ）
如图所示，轻质弹簧一端固定，另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连，弹簧水平且处于原长，圆环从A处由静止开始下滑，经过B处的速度最大，到达C处的速度为零，AC=h，圆环在C处获得一竖直向上的速度v，恰好能回到A，弹簧始终在弹性限度内，重力加速度为g，则圆环（ ）| A． | 下滑过程中，加速度一直减小 | |
| B． | 下滑过程中，克服摩擦力做的功为$\frac{1}{4}$mv2 | |
| C． | 在C处，弹簧的弹性势能为$\frac{1}{4}$mv2-mgh | |
| D． | 上滑经过B的速度大于下滑经过B的速度 |
7．宇航员王亚平在“天宮1号”飞船内进行了我国首次太空授课，演示了一些完全失重状态下的物理现象．若飞船质量为m，距地面高度为h，地球质量为M，半径为R，引力常量为G，则飞船所在处的重力加速度大小为（ ）
| A． | 0 | B． | $\frac{GM}{{{{（R+h）}^2}}}$ | C． | $\frac{GMm}{{{{（R+h）}^2}}}$ | D． | $\frac{GM}{h^2}$ |
6．
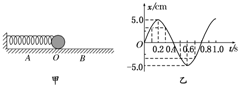如图甲所示为以O点为平衡位置，在A、B两点间做简谐运动的弹簧振子，图乙为这个弹簧振子的振动图象，由图可知下列说法中正确的是（ ）
如图甲所示为以O点为平衡位置，在A、B两点间做简谐运动的弹簧振子，图乙为这个弹簧振子的振动图象，由图可知下列说法中正确的是（ ）| A． | 在t=0.2s时，弹簧振子的加速度为正向最大 | |
| B． | 在t=0.1s与t=0.3s两个时刻，弹簧振子在同一位置 | |
| C． | 从t=0到t=0.2s时间内，弹簧振子做加速度增加的减速运动 | |
| D． | 在t=0.6s时，弹簧振子有最小的弹性势能 |
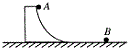如图所示，质量为2m、高度为h的光滑弧形槽末端水平，放置在光滑水平地面上，质量为m的小球A从弧形槽顶端静止释放，之后与静止在水平面上质量为m的小球B发生对心碰撞并粘在一起．求：
