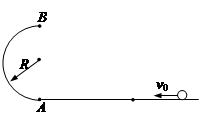题目内容
如右图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为α,已知该星球半径为R,万有引力常量为G,求: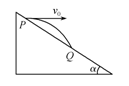
(1)该星球表面的重力加速度;
(2)该星球的密度;
(3)该星球的第一宇宙速度;
(4)人造卫星绕该星球做匀速圆周运动的最小周期.
(1)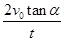 (2)
(2)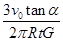 (3)
(3)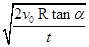 (4)2πR
(4)2πR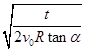
解析试题分析:(1)由平抛运动规律得,
tanα= ,则g=
,则g=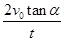 .
.
(2)在星球表面有:G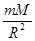 =mg,所以M=
=mg,所以M=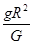 .该星球的密度:ρ=
.该星球的密度:ρ= =
=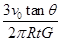 .
.
(3)由G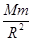 =m
=m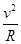 可得
可得
v=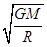 ,又GM=gR2
,又GM=gR2
所以v=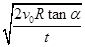 .
.
(4)绕星球表面运行的卫星具有最小的周期,即
T=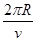 =2πR
=2πR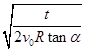 .
.
考点:此题考查万有引力定律及牛顿定律;平抛运动。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
如图所示,小车上有一定滑轮,跨过定滑轮的绳上一端系一重球,另一端系在弹簧秤上,弹簧秤固定在小车上。开始时小车处于静止状态,当小车匀加速向右运动时( )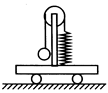
| A.弹簧秤读数及小车对地面压力均增大 |
| B.弹簧秤读数及小车对地面压力均变小 |
| C.弹簧秤读数变大,小车对地面的压力不变 |
| D.弹簧秤读数不变,小车对地面的压力变大 |
如图所示,在竖直平面内有一个半径为R的圆弧轨道。半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力,已知PA=2R,重力加速度为g,则小球 ( )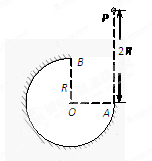
| A.从B点飞出后恰能落到A点 |
| B.从P到B的运动过程中机械能守恒 |
C.从P到B的运动过程中合外力做功 mgR mgR |
| D.从P到B的运动过程中克服摩擦力做功mgR |
2013 年2 月15日,俄罗斯车里雅宾斯克州发生陨石坠落事件。据俄科学院估计,陨石以不低于54000 公里的时速(即15km/s )进人大气层。陨石在靠近地球但未进入大气层之前,以下说法正确的是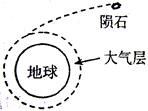
| A.机械能越来越大 |
| B.加速度越来越大 |
| C.速度越来越大 |
| D.若速度方向合适,陨石可被地球俘获绕地球做匀速圆周运动 |
用40 N的水平力F拉一个静止在光滑水平面上、质量为20 kg的物体,力F作用3 s后撤去,则第5 s末物体的速度和加速度的大小分别是( )
| A.v=6 m/s,a=0 | B.v=10 m/s,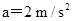 |
C.v=6 m/s,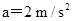 | D.v=10 m/s,a=0 |
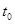 至
至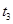 时间段内,弹簧秤的示数如图所示,电梯运行的v-t图可能是(取电梯向上运动的方向为正)
时间段内,弹簧秤的示数如图所示,电梯运行的v-t图可能是(取电梯向上运动的方向为正) 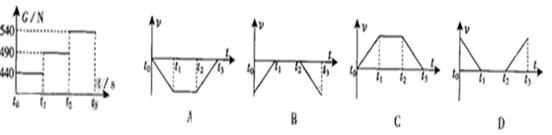
 B.
B.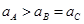
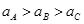 D.
D.