题目内容
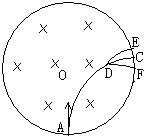（2004?惠州一模）如图所示，在一个半径为R的圆形区域内存在着匀强磁场，磁场方向垂直于圆面向里，一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内，粒子将做圆周运动到达磁场边界的C点，但在粒子经过D点时，恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子，关于这个新粒子的运动情况，以下判断正确的是（ ）分析：带电粒子在磁场中做匀速圆周运动，碰撞过程遵守动量守恒．根据动量守恒定律可知，碰撞后动量不变，但质量变大，共同速度变小，粒子在磁场中圆周运动半径公式r=
=
，P是动量．带电量不变，根据圆周运动半径和周期公式即可求解．
| mv |
| qB |
| P |
| qB |
解答：解：A、B、C根据动量守恒定律可知，碰撞后碰撞后动量不变，但质量变大，共同速度变小，带电量不变，则
r=
=
，其中动量P=mv不变，B不变，q不变，所以粒子的运动半径r不变，仍然到达C点．故AB错误，C正确；
D、根据周期公式T=
可知：碰撞后m变大，B、q不变，所以T变大，而粒子运动的轨迹不变，所以运动时间变长，故D错误．
故选C
r=
| mv |
| qB |
| P |
| qB |
D、根据周期公式T=
| 2πm |
| qB |
故选C
点评：本题主要考查了动量守恒定律及圆周运动半径和周期公式的直接应用，关键要抓住碰撞过程动量守恒进行分析，属于基础题．
练习册系列答案
相关题目
（2004?惠州一模）两个振动情况完全一样的波源S1、S2相距6m，它们在空间产生的干涉图样如图所示，图中实线表示振动加强区域，虚线表示振动减弱区域，下列说法正确的是（ ）