题目内容
(2004?惠州一模)晴天晚上,人能看见卫星的条件是卫星被太阳照着且在人的视野之内.一个可看成漫反射体的人造地球卫星的圆形轨道与赤道共面,卫星自西向东运动.春分期间太阳垂直射向赤道,赤道上某处的人在日落后8小时时在西边的地平线附近恰能看到它,之后极快地变暗而看不到了.已知地球的半径R地=6.4×106m,地面上的重力加速度为10m/s2,估算:(答案要求精确到两位有效数字)
(1)卫星轨道离地面的高度.
(2)卫星的速度大小.
(1)卫星轨道离地面的高度.
(2)卫星的速度大小.
分析:1、作出几何关系图,日落8小时Q点转过的角度θ=
×360°=120°,根据几何关系求解即可.
2、先根据万有引力等于重力解出卫星处的重力加速度,根据重力提供向心力列式,即可求出卫星的速度大小.
| 8 |
| 24 |
2、先根据万有引力等于重力解出卫星处的重力加速度,根据重力提供向心力列式,即可求出卫星的速度大小.
解答: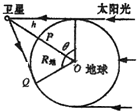 解:(1)从北极沿地轴往下看的地球俯视图如图所示,
解:(1)从北极沿地轴往下看的地球俯视图如图所示,
设卫星离地高h,Q点日落后8小时时能看到它反射的阳光.
日落8小时Q点转过的角度设为θ,
θ=
×360°=120°
轨道高h=
-R地
=6.4×106×(
-1)=6.4×106m
(2)地面处,重力等于万有引力mg=G
卫星处,mgr=G
两式相比得
=(
)2
因为卫星轨道半径r=R地+h=2R地
所以,gr=
g地=2.5m/s2
又因为,mgr=m
解得v=
=
=5.7×103m/s
答:(1)卫星轨道离地面的高度等于地球的半径,为6.4×106m.
(2)卫星的速度大小5.7×103m/s.
 解:(1)从北极沿地轴往下看的地球俯视图如图所示,
解:(1)从北极沿地轴往下看的地球俯视图如图所示,设卫星离地高h,Q点日落后8小时时能看到它反射的阳光.
日落8小时Q点转过的角度设为θ,
θ=
| 8 |
| 24 |
轨道高h=
| R地 | ||
cos
|
=6.4×106×(
| 1 |
| cos600 |
(2)地面处,重力等于万有引力mg=G
| Mm |
| R地2 |
卫星处,mgr=G
| Mm |
| (R地+h)2 |
两式相比得
| gr |
| g |
| R地 |
| R地+h |
因为卫星轨道半径r=R地+h=2R地
所以,gr=
| 1 |
| 4 |
又因为,mgr=m
| v2 |
| r |
解得v=
| grr |
| 2.5×2×6.4×106 |
答:(1)卫星轨道离地面的高度等于地球的半径,为6.4×106m.
(2)卫星的速度大小5.7×103m/s.
点评:本题考查了万有引力在天体中的应用,解题的关键在于找出向心力的来源,并能列出等式解题.对于卫星与地球的运动关系,要画出几何关系图,根据几何关系求解.

练习册系列答案
相关题目
 (2004?惠州一模)两个振动情况完全一样的波源S1、S2相距6m,它们在空间产生的干涉图样如图所示,图中实线表示振动加强区域,虚线表示振动减弱区域,下列说法正确的是( )
(2004?惠州一模)两个振动情况完全一样的波源S1、S2相距6m,它们在空间产生的干涉图样如图所示,图中实线表示振动加强区域,虚线表示振动减弱区域,下列说法正确的是( )