题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
A与B刚发生第一次碰撞后,A停下不动,B以初速v0向右运动.由于摩擦,B向右作匀减速运动,而C向右作匀加速运动,两者速率逐渐接近.设B、C达到相同速度v1时B移动的路程为s1.设A、B、C质量皆为m,由动量守恒定律,得mv0=2mv1 由动能定理得 得 根据条件 因此在B、C达到相同速度v1时,B尚未与A发生第二次碰撞.B与C一起将以v1向右匀速运动一段距离(L-S1)后才与A发生第二次碰撞.从A、B发生第一次碰撞后,到发生第二次碰撞所需的时间为
|
(2) |
A、B、C最后达到相同速度v2.由动量守恒定律,得 mv0=3m2 解得 凹槽A对木块B能做的总功的大小等于木块B对凹槽A所做总功的大小 对凹槽A应用动能定理
所以凹槽A对木块B能做的总功为
|

练习册系列答案
相关题目
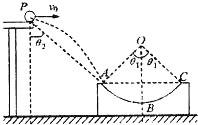 如图所示,圆弧形凹槽固定在水平地面上,其中ABC是以O为圆心的一段圆弧,位于竖直平面内.现有一质量为m的小球(可视为质点),从一水平桌面的边缘p点以速度v0向右水平飞出,该小球恰好能从A点沿圆弧的切线方向进入轨道,运动到C点速度减小为零.OA、OC与竖直方向的夹角均为θ1 PA与竖直方向的夹角为θ2.下列说法正确的是( )
如图所示,圆弧形凹槽固定在水平地面上,其中ABC是以O为圆心的一段圆弧,位于竖直平面内.现有一质量为m的小球(可视为质点),从一水平桌面的边缘p点以速度v0向右水平飞出,该小球恰好能从A点沿圆弧的切线方向进入轨道,运动到C点速度减小为零.OA、OC与竖直方向的夹角均为θ1 PA与竖直方向的夹角为θ2.下列说法正确的是( )| A、tanθ1.tanθ2=2 | ||
| B、小球进入A点时重力的瞬时功率为mgv0tanθ1 | ||
C、小球在圆形轨道内摩擦力做的功为
| ||
| D、小球在圆形轨道最低点B处受到轨道的支持力大小为mg |
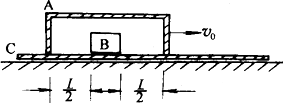
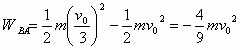
 如图所示,圆弧形凹槽固定在水平地面上,其中ABC是以O为圆心的一段圆弧,位于竖直平面内.现有一小球从一水平桌面的边缘P点向右水平飞出,该小球恰好能从A点沿圆弧的切线方向进入轨道.OA与竖直方向的夹角为θ1,PA与竖直方向的夹角为θ2.下列说法正确的是( )
如图所示,圆弧形凹槽固定在水平地面上,其中ABC是以O为圆心的一段圆弧,位于竖直平面内.现有一小球从一水平桌面的边缘P点向右水平飞出,该小球恰好能从A点沿圆弧的切线方向进入轨道.OA与竖直方向的夹角为θ1,PA与竖直方向的夹角为θ2.下列说法正确的是( )
