题目内容
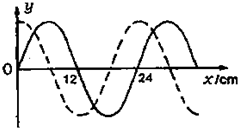 如图为一列简谐横波在两个不同时刻的波形,虚线为实线所示的横波在△t=0.5s后的波形图线,试求:
如图为一列简谐横波在两个不同时刻的波形,虚线为实线所示的横波在△t=0.5s后的波形图线,试求:(1)该波可能的传播速度?
(2)若质点的振动周期T与△t的关系为2T<△t<3T,则向前传播的波速各为多少?
(3)若波速为v=1.8m/s,则波向哪个方向传播?为什么(计算说明)?
分析:(1)若波沿x轴正方向传播,传播的最短距离为6m,若波沿x轴负方向传播,传播的最短距离为18m,根据波的周期性:相隔整数倍周期的时间,波形相同,根据时间与周期关系的通项,求出周期,从而确定可能传播速度.
(2)简谐波传播过程中,振动在一个周期内传播一个波长的距离.根据波形的平移法可知,若波向左传播,且2T<△t<3T,波传播的距离是2
λ;若波向右传播,且2T<△t<3T,波传播的距离是2
λ;即可由v=
求出波速.
(2)波速为v=1.8m/s和时间△t=0.5s,求出波传播的距离,根据波形的平移法判断波的传播方向.
(2)简谐波传播过程中,振动在一个周期内传播一个波长的距离.根据波形的平移法可知,若波向左传播,且2T<△t<3T,波传播的距离是2
| 1 |
| 4 |
| 3 |
| 4 |
| △x |
| △t |
(2)波速为v=1.8m/s和时间△t=0.5s,求出波传播的距离,根据波形的平移法判断波的传播方向.
解答:解:(1)设波的周期为T.若波沿x轴正方向传播,则:
t=(n+
)T1,
得:T1=
=
s (n=0,1,2,…)
传播的速度为:v1=
=
(4n+1)=0.12(4n+1)m/s
若波沿x轴负方向传播,则:t=(n+
)T2,
得:T2=
=
s (n=0,1,2,…)
传播的速度为:v2=
=
(4n+3)=0.12(4n+3)m/s
(2)由图知,波长λ=24cm;
若波向左传播,且2T<△t<3T,波传播的距离是△x=2
λ=54cm,波速为:v=
=
=108cm/s;
若波向右传播,且2T<△t<3T,波传播的距离是△x=2
λ=66cm,波速为:v═
=
=132cm/s;
(2)若波速为v=1.8m/s,波在△t内波传播的距离为:△x=v△t=1.8×0.5m=0.9m=90cm;
得:n=
=
=3
,根据波形的平移法得知,波向右传播.
答:(1)该波可能的传播速度向右为0.12(4n+1)m/s;向左为0.12(4n+3)m/s;
(2)若质点的振动周期T与△t的关系为2T<△t<3T,则向前传播的波速,向左传播速度为108cm/s;向右传播速度为132cm/s;
(3)若波速为v=1.8m/s,则波向右方向传播.
t=(n+
| 1 |
| 4 |
得:T1=
| 4t |
| 4n+1 |
| 2 |
| 4n+1 |
传播的速度为:v1=
| λ |
| T1 |
| 0.24 |
| 2 |
若波沿x轴负方向传播,则:t=(n+
| 3 |
| 4 |
得:T2=
| 4t |
| 4n+3 |
| 2 |
| 4n+3 |
传播的速度为:v2=
| λ |
| T2 |
| 0.24 |
| 2 |
(2)由图知,波长λ=24cm;
若波向左传播,且2T<△t<3T,波传播的距离是△x=2
| 1 |
| 4 |
| △x |
| △t |
| 54 |
| 0.5 |
若波向右传播,且2T<△t<3T,波传播的距离是△x=2
| 3 |
| 4 |
| △x |
| △t |
| 66 |
| 0.5 |
(2)若波速为v=1.8m/s,波在△t内波传播的距离为:△x=v△t=1.8×0.5m=0.9m=90cm;
得:n=
| △x |
| λ |
| 90 |
| 24 |
| 3 |
| 4 |
答:(1)该波可能的传播速度向右为0.12(4n+1)m/s;向左为0.12(4n+3)m/s;
(2)若质点的振动周期T与△t的关系为2T<△t<3T,则向前传播的波速,向左传播速度为108cm/s;向右传播速度为132cm/s;
(3)若波速为v=1.8m/s,则波向右方向传播.
点评:本题是波动图象中典型的问题,要根据波的周期性和双向性研究时间与周期的关系,关键根据波的周期性,得到得到波传播的距离,即可求得波速.根据波传播的距离与波长关系,是判断波的传播方向常用的方法.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 如图为一列简谐横波在某一时刻的波形图,此时刻质点F的运动方向如图所示,则( )
如图为一列简谐横波在某一时刻的波形图,此时刻质点F的运动方向如图所示,则( )| A、该波向左传播 | B、质点B和D的运动方向相同 | C、该波向右传播 | D、此时质点F和H的回复力不相同 |

 如图为一列简谐横波在某时刻的波形图,已知质点P此时的运动方向如图所示,则可判定( )
如图为一列简谐横波在某时刻的波形图,已知质点P此时的运动方向如图所示,则可判定( )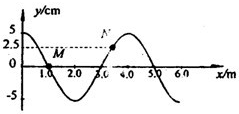 如图为一列简谐横波在t1=0时刻的波形图象,此时波中质点M正处于平衡位置,运动方向沿y轴负方向,到t2=0.55s时质点M恰好第三次到达y轴正方向最大位移处.试求:
如图为一列简谐横波在t1=0时刻的波形图象,此时波中质点M正处于平衡位置,运动方向沿y轴负方向,到t2=0.55s时质点M恰好第三次到达y轴正方向最大位移处.试求: