题目内容

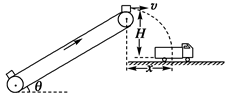
（12分）如图所示，传送带与地面倾角θ=37°，AB长为16米，传送带以10米/秒的速度逆时针匀速运动。在传送带上端A无初速地释放一个质量为0.5千克的物体，它与传送带之间的动摩擦系数为μ=0.5，求：（1）物体从A运动到B所需时间，（2）物体从A 运动到B 的过程中，摩擦力对物体所做的功（g=10米/秒2）.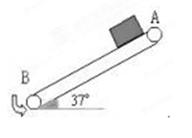

（1）2s     (2) -12J

解析试题分析：（1）当物体下滑速度小于传送带时，物体的加速度为a1，（此时滑动摩擦力沿斜面向下）则
a1=(mgsinθ+µmgcosθ)/m=10m/s2
t1=v/a1=1s
s1=a1t12/2=5m
当物体下滑速度大于传送带v=10m/s时，物体的加速度为a2(此时f沿斜面向上)，则
a2=(mgsinθ-µmgcosθ)/m=2m/s2
s1=vt2+a2t22/2=(a1t1)t2+ a2t22/2=11m
即10t2+t22=11解得t2=1s （t2=-11s舍去）
所以t=t1+t2=2s
(2)w1=fs1=µmgcosθs1=10J
W2=-fs2=-µmgcosθs2=-22J
W=w1+w2=-12J
考点：本题考查牛顿第二定律、运动学关系、总功的计算。

练习册系列答案
相关题目

一长木板在水平地面上运动，在t=0时刻将一相对于地面静止的物块轻放到木板上，以后木板运动的速度-时间图象如图中实线所示，0~0.5 s内物块运动的速度-时间图象如图中粗虚线所示．己知物块与木板的质量相等，物块与木板间及木板与地面间均有摩擦，物块与木板间的最大静摩擦力等于滑动摩擦力，且物块始终在木板上．取重力加速度的大小g="10" m/s2，求：

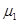（1）物块与木板间动摩擦因数、木板与地面间的动摩擦因数；
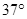（2）从t=0时刻到物块与木板均停止运动时，物块相对于木板的位移的大小．

两根完全相同的光滑细直杆上各套有一个完全相同的小球，且两杆均与水平面成角放置，将两小球均从离地面10m高处由静止释放，如图甲、乙所示。在水平向右的风力作用下，A球保持静止，B球沿细直杆下滑。求B球滑到地面所需的时间。（结果保留三位有效数字）（）

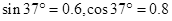（15分）如图所示，从A点以v0=4m/s的水平速度抛出一质量m=1kg的小物块（可视为质点），当物块运动至B点时，恰好沿切线方向进入光滑圆弧轨道BC，经圆弧轨道后滑上与C点等高、静止在粗糙水平面的长木板上，圆弧轨道C端切线水平。已知长木板的质量M＝4kg，A、B两点距C点的高度分别为H＝0.6m、h=0.15m，R＝0.75m，物块与长木板之间的动摩擦因数μ1＝0.5，长木板与地面间的动摩擦因数μ1＝0.2，g=10m/s2。求：

（1）小物块运动至B点时的速度大小和方向；
（2）小物块滑动至C点时，对圆弧轨道C点的压力；
（3）长木板至少为多长，才能保证小物块不滑出长木板?

（10分）在公路的十字路口, 红灯拦停了很多汽车, 拦停的汽车排成笔直的一列, 最前面的一辆汽车的前端刚好与路口停车线相齐, 相邻两车的前端之间的距离均为l =" 6.0" m，若汽车起动时都以a =2.5m/s2 的加速度作匀加速运动, 加速到v="10.0" m/s 后做匀速运动通过路口。该路口亮绿灯时间t =" 40.0" s, 而且有按倒计时显示的时间显示灯。 另外交通规则规定：原在绿灯时通行的汽车，红灯亮起时, 车头已越过停车线的汽车允许通过。请解答下列问题：
（1）若绿灯亮起瞬时，所有司机同时起动汽车，问有多少辆汽车能通过路口？
（2）第(1)问中, 不能通过路口的第一辆汽车司机，在时间显示灯刚亮出“3”时开始刹车做匀减速运动, 结果车的前端与停车线相齐时刚好停下, 求刹车后汽车加速度大小。
（3）事实上由于人反应时间的存在, 绿灯亮起时不可能所有司机同时起动汽车。现假设绿灯亮起时，第一个司机迟后Dt=0.90s起动汽车，后面司机都比前一辆车迟后0. 90s起动汽车，在该情况下，有多少辆车能通过路口？

质量为1000kg的汽车在200m长的平直跑道做启动、制动性能测试.汽车从跑道一端由静止开始匀加速运动，离终点还有40m时关闭发动机做匀减速运动.当汽车恰好停在跑道另一端时.全程运动时间为20s。假设汽车运动中所受阻力恒定.求：
(1)汽车关闭发动机时的速度；
(2)加速阶段汽车发动机应保持的牵引力大小？

如图是利用传送带装运煤块的示意图．其中，传送带足够长，倾角θ＝37°，煤块与传送带间的动摩擦因数μ＝0.8，传送带的主动轮和从动轮半径相等，主动轮轴顶端与运煤车底板间的竖直高度H＝1.8m，与运煤车车箱中心的水平距离x＝1.2m.现在传送带底端由静止释放一些煤块(可视为质点)，煤块在传送带的作用下先做匀加速直线运动，后与传送带一起做匀速运动，到达主动轮时随轮一起匀速转动．使煤块在轮的最高点恰好水平抛出并落在车箱中心，取g＝10m/s2，sin37°＝0.6，cos37°＝0.8，求：

(1)传送带匀速运动的速度v
(2)主动轮和从动轮的半径R；
(3)煤块在传送带上由静止开始加速至与传送带速度相同所经过的时间t.

如图所示，物体由静止从A点沿斜面匀加速下滑，随后在水平面上作匀减速运动，最后停止于C点，已知AB =" 4" m，BC =" 6" m，整个运动历时10 s，求分别在AB和BC运动的加速度．

有一个长L=4m、倾角为θ=370的斜面，底端有一垂直斜面的挡板。有一质量m=1kg的小物块从顶端A由静止沿斜面下滑，碰到挡板时的速度v=4m/s。若小物块从顶端A由静止沿斜面下滑到某点B（图中未标出）时，对其施加一平行于斜面向上的恒力F=10N，使小物块恰好不撞到挡板上。（g=10m/s2，sin37°=0.6，cos37°=0.8）求：

（1）物块A与斜面间的动摩擦因数；
（2）B点到挡板的距离。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网