题目内容
2. 质点沿直线运动,在10s内其速度由10m/s减为0,速度随时间变化的关系图象即v-t图象如图所示,恰好是以坐标原点为圆心的四分之一圆弧.则该质点在第6s末时的加速度为( )
质点沿直线运动,在10s内其速度由10m/s减为0,速度随时间变化的关系图象即v-t图象如图所示,恰好是以坐标原点为圆心的四分之一圆弧.则该质点在第6s末时的加速度为( )| A. | -$\frac{3}{4}$m/s2 | B. | -$\frac{\sqrt{2}}{2}$m/s2 | C. | -1m/s2 | D. | -$\frac{\sqrt{3}}{3}$m/s2 |
分析 速度-时间图象的斜率表示加速度,作出t=6s与圆的交点处的切线,根据几何关系求出斜率即可.
解答 解:作出t=6s与圆的交点处的切线BC,切点为A,如图所示:
根据几何关系可知:∠OAD=∠CBO,∠ADO=∠BOC,
则△OAD∽△CBO
所以$\frac{OC}{OB}=\frac{OD}{AD}=\frac{6}{\sqrt{1{0}^{2}-{6}^{2}}}=\frac{3}{4}$,
速度-时间图象的斜率表示加速度,CB的斜率k=$-\frac{3}{4}$,所以该质点在第6s末时的加速度a=-$\frac{3}{4}$m/s2,故A正确.
故选:A
点评 本题的关键是知道速度-时间图象斜率的物理意义,要求同学们能根据几何关系正确求出斜率,并且注意加速度是负值,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.汽车车以10m/s的速度在平直公路上匀速行驶,刹车后经2s速度变为6m/s,
(以初速度方向为正方向)求:
(1)刹车后过程中的加速度;
(2)刹车后前进9m所用的时间;
(3)刹车后6s内前进的距离.
(以初速度方向为正方向)求:
(1)刹车后过程中的加速度;
(2)刹车后前进9m所用的时间;
(3)刹车后6s内前进的距离.
13.探究功与物体速度变化的关系实验中,下列叙述正确的是( )


| A. | 每次实验必须设法算出橡皮筋对小车做功的具体数值 | |
| B. | 该实验不用平衡小车受到的摩擦力 | |
| C. | 每次实验中应使小车从同一位置由静止出发 | |
| D. | 实验打出纸带后,应选取纸带上点迹间隔均匀的一段测量小车的速度 |
14.若忽略空气阻力,质量不同的小球从同一高度同时做自由落体运动,则( )
| A. | 质量大的下落得快 | B. | 质量小的下落得快 | ||
| C. | 质量不同的下落一样快 | D. | 质量不同的加速度不同 |
 如图所示,变阻器R0的滑片P从最左端移到最右端时理想电压表的示数变化范围是0~4V,理想电流表的示数变化范围是1.5A~0.5A,电源的内阻忽略不计,求电阻R的阻值、变阻器R0的最大阻值和电源电压U.
如图所示,变阻器R0的滑片P从最左端移到最右端时理想电压表的示数变化范围是0~4V,理想电流表的示数变化范围是1.5A~0.5A,电源的内阻忽略不计,求电阻R的阻值、变阻器R0的最大阻值和电源电压U. 如图所示,质量m=15kg的木箱静止在水平地面上,木箱与地面间的动摩擦因数μ=0.2.现用F=60N的水平恒力向右拉动木箱(g=10m/s2).求:
如图所示,质量m=15kg的木箱静止在水平地面上,木箱与地面间的动摩擦因数μ=0.2.现用F=60N的水平恒力向右拉动木箱(g=10m/s2).求: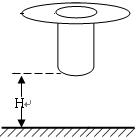 有一个小圆环瓷片最高能从h=0.18m高处静止释放后直接撞击地面而不被摔坏.现让该小圆环瓷片恰好套在一圆柱体上端且可沿圆柱体下滑,瓷片与圆柱体之间的摩擦力是瓷片重力的4.5倍,如图所示.若将该装置从距地面H=4.5m高处从静止开始下落,瓷片落地恰好没摔坏.已知圆柱体与瓷片所受的空气阻力都为自身重力的0.1倍,圆柱体碰地后速度立即变为零且保持竖直方向.(g=10m/s2)
有一个小圆环瓷片最高能从h=0.18m高处静止释放后直接撞击地面而不被摔坏.现让该小圆环瓷片恰好套在一圆柱体上端且可沿圆柱体下滑,瓷片与圆柱体之间的摩擦力是瓷片重力的4.5倍,如图所示.若将该装置从距地面H=4.5m高处从静止开始下落,瓷片落地恰好没摔坏.已知圆柱体与瓷片所受的空气阻力都为自身重力的0.1倍,圆柱体碰地后速度立即变为零且保持竖直方向.(g=10m/s2)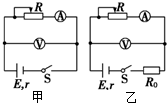 如图甲是“测电池的电动势和内阻”的实验电路,如果采用新电池进行实验,实验时会发现,当滑动变阻器在阻值较大的范围内调节时,电压表变化很小,原因是:新电池的内阻很小,内电路分得的内电压很小,从而影响测量值的精确性.为了较精确地测量一节新电池的内阻,可用以下给定的器材和一些导
如图甲是“测电池的电动势和内阻”的实验电路,如果采用新电池进行实验,实验时会发现,当滑动变阻器在阻值较大的范围内调节时,电压表变化很小,原因是:新电池的内阻很小,内电路分得的内电压很小,从而影响测量值的精确性.为了较精确地测量一节新电池的内阻,可用以下给定的器材和一些导 如图所示,水平地面上的L形木板M上放着小木块m,M与m间有一处于压缩状态的弹簧,整个装置处于静止状态.长木板受力的个数为( )
如图所示,水平地面上的L形木板M上放着小木块m,M与m间有一处于压缩状态的弹簧,整个装置处于静止状态.长木板受力的个数为( )