题目内容
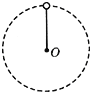
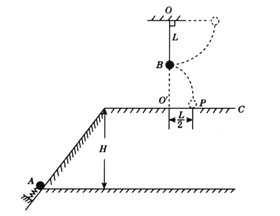
【题目】如图所示，在同一竖直平面上，质量为2m的小球A静止在光滑斜面的底部，斜面高度为H＝2L。小球受到弹簧的弹力作用后，沿斜面向上运动。 离开斜面后，达到最高点时与静止悬挂在此处的小球B发生弹性碰撞，碰撞后球B刚好能摆到与悬点O同一高度，球A沿水平方向抛射落在水平面C上的P点，O点的投影O′与P的距离为L/2。已知球B的质量为m，悬绳长L，初始时离O′高度为L，视两球为质点。重力加速度为g，不计空气阻力。求：
(1)球B在两球碰撞后一瞬间的速度大小；
(2)球A在两球碰撞前一瞬间的速度大小；
(3)弹簧的弹力对球A所做的功；
【答案】（1）
（2）
（3）
【解析】（1）碰撞后，根据机械能守恒定律，对B球有： 
解得： 
即球B在两球碰撞后一瞬间的速度大小为
．
（2）碰后A球做平抛运动，根据平抛运动的规律得
两球碰撞后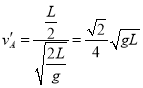
，
规定向右为正方向，A、B球碰撞水平方向动量守恒有： 
解得
（3）弹簧的弹力对球A所做的功W，对球A和弹簧组成的系统，由机械能守恒定律： 
练习册系列答案
名校课堂系列答案
相关题目
