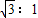题目内容
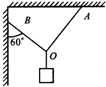
 如图所示,相同的细绳OA、OB共同吊起质量m的物体.OA与OB相垂直.OB竖直墙壁成600角,OA、OB对O点的拉力分别为Tl、T2,则( )
如图所示,相同的细绳OA、OB共同吊起质量m的物体.OA与OB相垂直.OB竖直墙壁成600角,OA、OB对O点的拉力分别为Tl、T2,则( )分析:以结点O为研究对象,分析受力情况,采用正交分解法研究Tl、T2水平方向的分力的关系及Tl、T2竖直方向的合力与重力的关系.根据平衡条件求出Tl:T2.若逐渐增加m的质量,所受拉力较大的绳子先断.
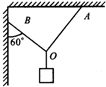
解答:解:以结点O为研究对象,分析受力情况,如图.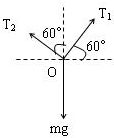
A、根据正交分解法得知:Tl、T2水平方向的分力之比为1:1.故A错误.
B、结点O受到三个力:mg、Tl、T2,根据平衡条件得到Tl、T2竖直方向的合力等于mg.故B正确.
C、由水平方向力平衡得:
T1cos60°=T2sin60°,得到Tl、T2之比Tl:T2=
:1.故C错误.
D、由上得知,Tl>T2,即OA绳的拉力较大,若逐渐增加m的质量,OA绳一定先断.故D错误.
故选B

A、根据正交分解法得知:Tl、T2水平方向的分力之比为1:1.故A错误.
B、结点O受到三个力:mg、Tl、T2,根据平衡条件得到Tl、T2竖直方向的合力等于mg.故B正确.
C、由水平方向力平衡得:
T1cos60°=T2sin60°,得到Tl、T2之比Tl:T2=
| 3 |
D、由上得知,Tl>T2,即OA绳的拉力较大,若逐渐增加m的质量,OA绳一定先断.故D错误.
故选B
点评:对于悬绳类型的问题,常常以结点为研究对象,可采用正交分解法和合成法结合研究本题,比较简便.

练习册系列答案
相关题目