题目内容
如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，y轴为两种场的分界面，图中虚线为磁场区域的右边界，现有一质量为m，电荷量为-q的带电粒子从电场中坐标位置（-l，0）处，以初速度v0，沿x轴正方向开始运动，且已知l=
。试求：使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d应满足的条件。
解析：带电粒子在电场中做类平抛运动，设运动的加速度为a，由牛顿运动定律得：qE= ma，设粒子出电场、入磁场时速度的大小为v，此时在y轴方向的分速度为vy，粒子在电场中运动的时间为t，则有：vy=at；l=v0t解得vy=v0，v=。
设v的方向与y轴的夹角为θ。则有cosθ=
得θ=45°。粒子进入磁场后在洛伦兹力作用下做圆周运动，如图所示，则有R=
。
由图中的几何关系可知，要使粒子穿越磁场区域，磁场的宽度条件为d＜R(1+cosθ)。
结合已知条件，解以上各式可得d＜
说明：对角度的表示可以有不同方式，只要结果正确均可。
答案：d＜
练习册系列答案
相关题目
（2011?青铜峡市一模）如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，y轴为两种场的分界面，图中虚线为磁场区的右边界．现有一质量为m．电量为-q的带电粒子，从电场中的P点以初速度V0沿x轴正方向开始运动，已知P点的坐标为（-L，0）且
（2007?河东区模拟）如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，y轴为两种场的分界面，图中虚线为磁场区域的右边界．现有一质量为m，电荷量为-q的带电粒子从电场中坐标位置（-L，0）处，以初速度v0沿x轴正方向开始运动，且已知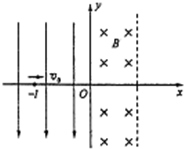
如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，y轴为两种场的分界线，图中虚线为磁场区域的右边界，现有一质量为m、电荷量为-q的带电粒子从电场中坐标位置（-l，0）处，以初速度v0沿x轴正方向开始运动，且已知
（重力不计）。试求：（1）带电粒子进入磁场时速度的大小？