题目内容
 (2007?河东区模拟)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区域的右边界.现有一质量为m,电荷量为-q的带电粒子从电场中坐标位置(-L,0)处,以初速度v0沿x轴正方向开始运动,且已知L=
(2007?河东区模拟)如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种场的分界面,图中虚线为磁场区域的右边界.现有一质量为m,电荷量为-q的带电粒子从电场中坐标位置(-L,0)处,以初速度v0沿x轴正方向开始运动,且已知L=m
| ||
| qE |
试求:要使带电粒子能穿越磁场区域而不再返回电场中,磁场的宽度d应满足的条件.
分析:粒子在电场中受到的电场力的方向向上,粒子做类平抛运动,水平方向做的是匀速运动,竖直方向做的是匀加速直线运动,从而可以求得带电粒子运动到Y轴上时的速度;当磁场的运动的轨迹恰好与磁场的右边沿相切时,此时的磁场的宽度最大,根据粒子的运动的轨迹可以求得磁场的宽度最大值.
解答:解:带电粒子在电场中做类平抛运动,设粒子进入磁场时的速度大小为v,速度方向与y轴的夹角为θ,如图所示,则:
vy=
?
=v0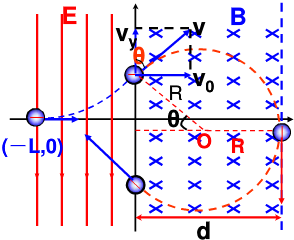
故
v=
=
v0
cosθ=
=
,θ=45°;
粒子在磁场中做匀速圆周运动的半径为:R=
要使带电粒子能穿越磁场区域,磁场的宽度应满足的条件为:d<(1+cosθ)R
即:d<
答:要使带电粒子能穿越磁场区域而不再返回电场中,磁场的宽度d应满足的条件为d<
.
vy=
| qE |
| m |
| L |
| v0 |

故
v=
|
| 2 |
cosθ=
| vy |
| v |
| ||
| 2 |
粒子在磁场中做匀速圆周运动的半径为:R=
| mv |
| qB |
要使带电粒子能穿越磁场区域,磁场的宽度应满足的条件为:d<(1+cosθ)R
即:d<
(1+
| ||
| qB |
答:要使带电粒子能穿越磁场区域而不再返回电场中,磁场的宽度d应满足的条件为d<
(1+
| ||
| qB |
点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2007?河东区模拟)质量均为5kg的物块1、2放在光滑水平面上并用轻质弹簧秤相连,如图所示,今对物块1、2分别施以方向相反的水平力F1、F2,且F1=20N,F2=10N,则弹簧秤的示数为( )
(2007?河东区模拟)质量均为5kg的物块1、2放在光滑水平面上并用轻质弹簧秤相连,如图所示,今对物块1、2分别施以方向相反的水平力F1、F2,且F1=20N,F2=10N,则弹簧秤的示数为( ) (2007?河东区模拟)如图所示,理想变压器的原线圈匝数为 n1=1000匝,副线圈匝数 n2=200匝,交变电源的电动势
(2007?河东区模拟)如图所示,理想变压器的原线圈匝数为 n1=1000匝,副线圈匝数 n2=200匝,交变电源的电动势 (2007?河东区模拟)如图所示,竖直平面内有两根很长的金属导轨MN、PQ,处于B=0.5T的水平匀强磁场中,两导轨中连有两个电阻均为0.2Ω.额定功率均为5W的小灯泡,如图所示.质量m=50g、长L=0.5m、电阻r=0.2Ω的金属棒ab可沿导轨做无摩擦滑动,导轨电阻不计.导轨与金属棒接触始终良好.则:
(2007?河东区模拟)如图所示,竖直平面内有两根很长的金属导轨MN、PQ,处于B=0.5T的水平匀强磁场中,两导轨中连有两个电阻均为0.2Ω.额定功率均为5W的小灯泡,如图所示.质量m=50g、长L=0.5m、电阻r=0.2Ω的金属棒ab可沿导轨做无摩擦滑动,导轨电阻不计.导轨与金属棒接触始终良好.则: (2007?河东区模拟)如图所示,有一质量为m的物块静止在水平桌面左端,长为L的细线竖直悬挂一个质量为2m的小球,小球刚好与物块接触.现保持细线绷直,把小球拉向左上方使细线与竖直方向成60°夹角,无初速释放,小球运动到最低点时恰与物块正碰,碰后小球继续向右摆动,上升的最大高度为
(2007?河东区模拟)如图所示,有一质量为m的物块静止在水平桌面左端,长为L的细线竖直悬挂一个质量为2m的小球,小球刚好与物块接触.现保持细线绷直,把小球拉向左上方使细线与竖直方向成60°夹角,无初速释放,小球运动到最低点时恰与物块正碰,碰后小球继续向右摆动,上升的最大高度为