题目内容
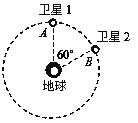
【题目】如图所示，两绳系一质量为m＝0.1kg的小球，上面绳长L＝2m，两端都拉直时与轴的夹角分别为30°与45°，问：
（1）球的角速度在什么范围内，两绳始终张紧。
（2）当角速度为3 rad／s时，上、下两绳拉力分别为多大？
【答案】（1）
（2）
【解析】试题分析：（1）当AC绳拉直但没有力时，BC绳子拉力的水平分力提供向心力，根据牛顿第二定律列式求出此时的角速度，当BC绳拉直但没有力时，AC绳子拉力的水平分力提供向心力，根据牛顿第二定律列式求出角速度，当角速度处于两者之间时，两绳均张紧；
（2）当ω=3rad/s时，AC、BC绳子拉力的水平分力的合力提供向心力，竖直方向分力之和与重力平衡，根据牛顿第二定律列式求解．
（1）当AC绳拉直但没有力时，即FT1=0时，由重力和绳BC的拉力FT2的合力提供向心力，根据牛顿第二定律，有： 
，其中： 
，
解得： 
当
恰为零时，根据牛顿第二定律，有： 
，解得
所以当
时两绳均张紧．
（2）当
时，两绳均处于张紧状态，此时小球受
、mg三力作用，正交分解后可得：
水平方向： 
竖直方向： 
代入数据后解得： 
阅读快车系列答案
【题目】如图为“测量弹簧劲度系数”的实验装置图，弹簧的上端固定在铁架台上，下端装有指针及挂钩，指针恰好指向一把竖直立起的毫米刻度尺．现在测得在挂钩上挂上一定数量钩码时指针在刻度尺上的读数如下表：
钩码数n | 0 | 1 | 2 | 3 | 4 | 5 |
刻度尺读数xn（cm） | 2．62 | 4．17 | 5．70 | 7．22 | 8．84 | 10．43 |
已知所有钩码的质量可认为相同且
，当地重力加速度
＝9．8 m/s2．
（1）请根据以上数据写出一种计算出弹簧的劲度系数的方法（不要求计算劲度系数的具体值）
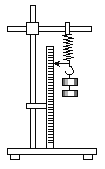
（2）考虑到在没有挂钩码时弹簧自身有重量，测量的劲度系数与真实值相比较________（填“偏大”、“偏小”或“没有影响”）．
