题目内容
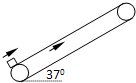 如图所示,传送带长6m,与水平方向的夹角37°,以5m/s的恒定速度向上运动.一个质量为2kg的物块(可视为质点),沿平行于传送带方向以10m/s的速度滑上传送带,已知物块与传送带之间的动摩擦因数μ=0.5,sin37°=0.6,cos37°=0.8,g=10m/s2.求:
如图所示,传送带长6m,与水平方向的夹角37°,以5m/s的恒定速度向上运动.一个质量为2kg的物块(可视为质点),沿平行于传送带方向以10m/s的速度滑上传送带,已知物块与传送带之间的动摩擦因数μ=0.5,sin37°=0.6,cos37°=0.8,g=10m/s2.求:(1)物块刚滑上传送带时的加速度大小;
(2)物块到达传送带顶端时的速度大小.
分析:(1)根据物体相对传送带滑动的方向确定出摩擦力的方向,结合牛顿第二定律求出物块刚滑上传送带时的加速度大小.
(2)根据速度时间公式以及位移公式求出物块速度达到传送带速度时的位移,判断物体在速度与传送带速度相等时,是否到达最高点,若未到达最高点,再结合牛顿第二定律求出加速度的大小,结合速度位移公式求出到达最高点的速度.
(2)根据速度时间公式以及位移公式求出物块速度达到传送带速度时的位移,判断物体在速度与传送带速度相等时,是否到达最高点,若未到达最高点,再结合牛顿第二定律求出加速度的大小,结合速度位移公式求出到达最高点的速度.
解答:解:(1)物块刚滑上传送带时,物块的加速度大小为a1,由牛顿第二定律有:
mgsin37°+μmgcos37°=ma1
代入数据解得:a1=gsin37°+μgcos37°=10×0.6+0.5×10×0.8=10m/s2;
(2)设物块速度减为5m/s所用时间为t1,则v0-v=a1t1
解得:t1=0.5s
通过的位移:x1=
?t1=
×0.5m=3.75m<6 m
因μ<tanθ,此后物块继续减速上滑的加速度大小为a2则:mgsin37°-μmgcos37°=ma2
代入数据解得:a2=2m/s2
设物块到达最高点的速度为v1,则:v2-v12=2a2x2
x2=l-x1=2.25m
解得:v1=4m/s.
答:(1)物块刚滑上传送带时的加速度大小为10m/s2;(2)物块到达传送带顶端时的速度为4m/s;
mgsin37°+μmgcos37°=ma1
代入数据解得:a1=gsin37°+μgcos37°=10×0.6+0.5×10×0.8=10m/s2;
(2)设物块速度减为5m/s所用时间为t1,则v0-v=a1t1
解得:t1=0.5s
通过的位移:x1=
| v+v0 |
| 2 |
| 10+5 |
| 2 |
因μ<tanθ,此后物块继续减速上滑的加速度大小为a2则:mgsin37°-μmgcos37°=ma2
代入数据解得:a2=2m/s2
设物块到达最高点的速度为v1,则:v2-v12=2a2x2
x2=l-x1=2.25m
解得:v1=4m/s.
答:(1)物块刚滑上传送带时的加速度大小为10m/s2;(2)物块到达传送带顶端时的速度为4m/s;
点评:解决本题的关键理清物块在传送带上的运动规律,结合牛顿第二定律和运动学公式灵活求解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目

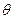 =37°角,以
=37°角,以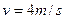 沿逆时针方向匀速传动,一质量为M=0.5kg的物块在传送带的顶端由静止释放,物块与传送带间的动摩擦因数为
沿逆时针方向匀速传动,一质量为M=0.5kg的物块在传送带的顶端由静止释放,物块与传送带间的动摩擦因数为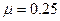 ,当物块滑到底端时,有一质量为m=0.01kg的子弹以
,当物块滑到底端时,有一质量为m=0.01kg的子弹以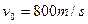 原速度射入物块,后又以
原速度射入物块,后又以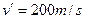 的速度穿出物块,以后每隔
的速度穿出物块,以后每隔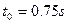 就有相同的子弹以相同的速度射入和穿出。(不计子弹穿过物块的时间,sin37°=0.6,cos37=0.8)
就有相同的子弹以相同的速度射入和穿出。(不计子弹穿过物块的时间,sin37°=0.6,cos37=0.8)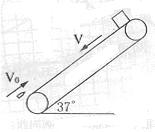
 ,以5 m/s的恒定速度向上运动。一个质量为2 kg的物块(可视为质点),沿平行于传送带方向以10 m/s的速度滑上传送带,已知物块与传送带之间的动摩擦因数μ=0.5,sin370=0.6,cos370=0.8,g=10m/s2。求:
,以5 m/s的恒定速度向上运动。一个质量为2 kg的物块(可视为质点),沿平行于传送带方向以10 m/s的速度滑上传送带,已知物块与传送带之间的动摩擦因数μ=0.5,sin370=0.6,cos370=0.8,g=10m/s2。求: