题目内容
5.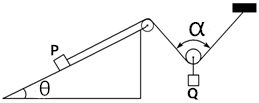 如图所示,固定斜面倾角θ=30°,轻绳一端通过两个滑轮与放在斜面上的物块P相连接,另一端固定在天花板上,不计绳与滑轮的摩擦及滑轮的质量.已知物块P的质量为m,在动滑轮上挂上物块Q后,连接物块的轻绳与斜面平行,当动滑轮两侧轻绳的夹角α=60°时,物块P、Q均保持静止.
如图所示,固定斜面倾角θ=30°,轻绳一端通过两个滑轮与放在斜面上的物块P相连接,另一端固定在天花板上,不计绳与滑轮的摩擦及滑轮的质量.已知物块P的质量为m,在动滑轮上挂上物块Q后,连接物块的轻绳与斜面平行,当动滑轮两侧轻绳的夹角α=60°时,物块P、Q均保持静止.(1)若斜面光滑,求物块Q的质量m;
(2)如物块P与斜面间的动摩擦因数μ恒为$\frac{\sqrt{3}}{6}$,其间的最大静摩擦力与滑动摩擦力大小相等,求物块Q的质量M应满足条件.
分析 (1)先对P受力分析,运用共点力平衡条件求出细线的拉力,再对Q受力分析,再次运用共点力平衡条件求Q的质量;
(2)若斜面与P之间有摩擦力,当摩擦力到达最大值且方向沿斜面向下时,绳子拉力最大,此时Q的质量最大,当摩擦力到达最大值且方向沿斜面向上时,绳子拉力最小,此时Q的质量最小,根据共点力平衡条件求出绳子的最大拉力和最小拉力,再对Q受力分析,根据平衡条件求出质量的范围.
解答 解:(1)若斜面光滑,先对P受力分析,根据共点力平衡条件得:
绳子拉力T=$mgsin30°=\frac{1}{2}mg$
再对Q受力分析,Q受到两根绳子的拉力以及重力作用,受力平衡,根据共点力平衡条件得:
2Tcos$\frac{α}{2}$=Mg
解得:M=$\frac{\sqrt{3}}{2}m$
(2)若斜面与P之间有摩擦力,当摩擦力到达最大值且方向沿斜面向下时,绳子拉力最大,此时Q的质量最大,
当摩擦力到达最大值且方向沿斜面向上时,绳子拉力最小,此时Q的质量最小,
根据共点力平衡条件得:
Tmax=mgsin30°+μmgcos30°=$\frac{3}{4}mg$,
${T}_{min}=mgsin30°-μmgcos30°=\frac{1}{4}mg$,
再对Q受力分析,Q受到两根绳子的拉力以及重力作用,受力平衡,根据共点力平衡条件得:
2Tmaxcos$\frac{α}{2}$=Mmaxg,
2Tmincos$\frac{α}{2}$=Mming,
解得:Mmax=$\frac{3\sqrt{3}}{4}m$,Mmin=$\frac{\sqrt{3}}{4}m$
则物块Q的质量M应满足条件为$\frac{\sqrt{3}}{4}m≤M≤\frac{3\sqrt{3}}{4}m$.
答:(1)若斜面光滑,物块Q的质量为$\frac{\sqrt{3}}{2}m$;
(2)如物块P与斜面间的动摩擦因数μ恒为$\frac{\sqrt{3}}{6}$,其间的最大静摩擦力与滑动摩擦力大小相等,则物块Q的质量M应满足条件为$\frac{\sqrt{3}}{4}m≤M≤\frac{3\sqrt{3}}{4}m$.
点评 本题关键是先后对物体P、Q受力分析,根据共点力平衡条件,结合合成法或正交分解法列式求解,知道当摩擦力到达最大值且方向沿斜面向下时,绳子拉力最大,此时Q的质量最大,当摩擦力到达最大值且方向沿斜面向上时,绳子拉力最小,此时Q的质量最小.

| A. | 10-1N | B. | 10-4 N | C. | 10-7 N | D. | 10-10 N |
 如图所示,杆BC的B端用铰链接于竖直墙上,另一端C为一定滑轮.重物G系一绳经过滑轮固定于墙上的A点,杆恰好平衡.若将绳的A端沿墙向上移,再使之平衡,杆重、滑轮大小及各处摩擦均可省略,则( )
如图所示,杆BC的B端用铰链接于竖直墙上,另一端C为一定滑轮.重物G系一绳经过滑轮固定于墙上的A点,杆恰好平衡.若将绳的A端沿墙向上移,再使之平衡,杆重、滑轮大小及各处摩擦均可省略,则( )| A. | 绳子的拉力增大,BC杆受到的压力增大 | |
| B. | 绳子的拉力增大,BC杆受到的压力减小 | |
| C. | 绳子的拉力不变,BC杆受到的压力不变 | |
| D. | 绳子的拉力不变,BC杆受到的压力减小 |

| A. | O 点的电场强度一定为零 | |
| B. | -x1 与-x2 点的电场强度相同 | |
| C. | -x1 和-x2两点在同一等势面上 | |
| D. | 将负电荷从-x1 移到 x1 电荷的电势能增大 |

 如图所示,半径为R的空心球壳,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过球壳球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块放入球壳内,经过一段时间后小物块随球壳一起转动且相对球壳静止,它和O点的连线与OO′之间的夹角θ为60°,重力加速度大小为g.
如图所示,半径为R的空心球壳,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过球壳球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块放入球壳内,经过一段时间后小物块随球壳一起转动且相对球壳静止,它和O点的连线与OO′之间的夹角θ为60°,重力加速度大小为g. 如图所示,在竖直平面内固定半径为R的光滑圆弧轨道与倾角θ=30°的粗糙斜轨相切于B点.一质量为m的小滑块(可视为质点)从导轨上离地面高为H=4R的A处无初速下滑,从圆弧最高点D水平飞出,恰好击中斜轨上与圆心O等高的E点,重力加速度为g.求:
如图所示,在竖直平面内固定半径为R的光滑圆弧轨道与倾角θ=30°的粗糙斜轨相切于B点.一质量为m的小滑块(可视为质点)从导轨上离地面高为H=4R的A处无初速下滑,从圆弧最高点D水平飞出,恰好击中斜轨上与圆心O等高的E点,重力加速度为g.求:
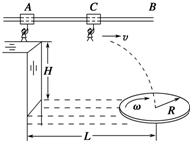 某电视台“快乐向前冲”节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,角速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.
某电视台“快乐向前冲”节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,角速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.