题目内容
如图所示,一固定光滑杆与水平方向夹角为 ,将一质量为
,将一质量为 的小环套在杆上,通过轻绳悬挂一个质量为
的小环套在杆上,通过轻绳悬挂一个质量为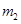 的小球,由静止释放后,小环与小球保持相对静止且以相同的加速度
的小球,由静止释放后,小环与小球保持相对静止且以相同的加速度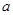 一起下滑,此时绳子与竖直方向夹角为
一起下滑,此时绳子与竖直方向夹角为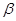 ,则下列说法正确的是( )
,则下列说法正确的是( )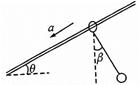
A.杆对小环的作用力大于 |
B. 不变,则 不变,则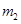 越大, 越大,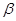 越小 越小 |
C.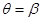 ,与 ,与 、 、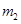 无关 无关 |
D.若杆不光滑,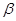 可能大于 可能大于 |
C
解析试题分析:以整体为研究对象,分析受力情况,如图: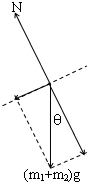
由牛顿第二定律得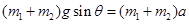 ,得
,得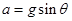 ,
, ;故A错误。再对小球研究可知,其合力大小为
;故A错误。再对小球研究可知,其合力大小为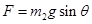 ,等于重力沿杆向下方向的分力,则细线与杆垂直,则由几何知识得,
,等于重力沿杆向下方向的分力,则细线与杆垂直,则由几何知识得,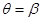 ,与环和小球的质量无关,故B错误、C正确。若杆不光滑;把环和球看做一个整体受力分析,沿斜面和垂直斜面建立直角坐标系得:沿斜面方向:
,与环和小球的质量无关,故B错误、C正确。若杆不光滑;把环和球看做一个整体受力分析,沿斜面和垂直斜面建立直角坐标系得:沿斜面方向: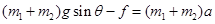 ,垂直斜面方向:
,垂直斜面方向: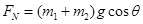 ,摩擦力:
,摩擦力: N,联立可解得:
N,联立可解得: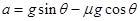 ,设
,设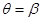 ,由几何关系知,此时绳应该和杆垂直,对小球受力分析可知重力沿杆的分力作为合力产生加速度,垂直于杆的分力与绳的拉力相平衡,此时可以求得小球的加速度为
,由几何关系知,此时绳应该和杆垂直,对小球受力分析可知重力沿杆的分力作为合力产生加速度,垂直于杆的分力与绳的拉力相平衡,此时可以求得小球的加速度为 ,大于整体的加速度
,大于整体的加速度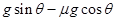 ,故绳的拉力要有一个分力来减小小球重力沿着杆方向的分力,所以绳应该向下倾斜,故
,故绳的拉力要有一个分力来减小小球重力沿着杆方向的分力,所以绳应该向下倾斜,故 ,故D错误。
,故D错误。
考点:本题考查了整体法与隔离法的受力分析、力的合成与分解、牛顿第二定律.

如图所示,光滑固定斜面的倾角为37°,QN垂直于斜面水平底边PQ,斜面上固定一个既垂直于斜面又垂直于QN的粗糙挡板.质量为m的小物块A置于挡板与斜面间,A与挡板间的动摩擦因数为μ,今施加平行于挡板和斜面的水平推力F,物块可沿挡板匀速滑动,则物块
| A.受斜面支持力N1=mgcos37° |
| B.所受挡板支持力N2=mgcos37° |
| C.所受推力F=μmgcos37° |
| D.所受推力F=μmgsin37° |
如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端。B与小车平板间的动摩擦因数为μ.若某过程中观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为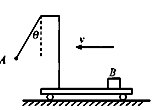
A.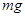 ,竖直向上 ,竖直向上 |
B.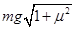 ,斜向左上方 ,斜向左上方 |
C.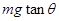 ,水平向右 ,水平向右 |
D.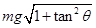 ,斜向右上方 ,斜向右上方 |
用一根长1 m的轻质细绳将一幅质量为1 kg的画框对称悬挂在墙壁上。已知绳能承受的最大张力为10 N。为使绳不断裂,画框上两个挂钉的间距最大为(g取10 m/s2)( )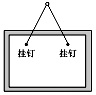
A.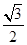 m m | B.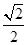 m m |
C.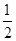 m m | D.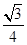 m m |
如图所示,有一质量不计的杆AO,长为R,可绕A自由转动.用绳在O点悬挂一个重为G的物体,另一根绳一端系在O点,另一端系在圆弧形墙壁上的C点.当点C由图示位置逐渐向上沿圆弧CB移动过程中(保持OA与地面夹角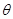 不变),OC绳所受拉力的大小变化情况是
不变),OC绳所受拉力的大小变化情况是
| A.逐渐减小 | B.逐渐增大 |
| C.先减小后增大 | D.先增大后减小 |
如图所示,一根轻质木棒AO,A端用光滑铰链固定于墙上,在O端下面吊一个重物,上面用细绳BO系于顶板上,现将B点逐渐向右移动,并使棒AO始终保持水平,则下列判断中正确的是:( )
| A.BO绳上的拉力大小不变 |
| B.BO绳上的拉力先变大后变小 |
| C.BO绳上的拉力对轻杆的力矩先变大后变小 |
| D.BO绳上的拉力对轻杆的力矩不变 |
如图所示,在光滑水平面上有一质量为M的斜劈,其斜面倾角为α,一质量为m的物体放在其光滑斜面上,现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,则斜劈对物块m的弹力大小为:( )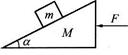
| A.mgcosα | B.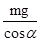 |
C.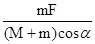 | D.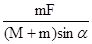 |
作用于O点的五个恒力的矢量图的末端跟O点恰好构成一个正六边形,如图所示。这五个恒力的合力是最大恒力的( )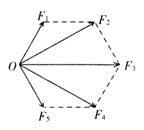
| A.2倍 | B.3倍 | C.4倍 | D.5倍 |
如图所示,一运送救灾物资的直升飞机沿水平方向匀速飞行.已知物资的总质量为m,吊运物资的悬索与竖直方向成θ角.设物资所受的空气阻力为f,悬索对物资的拉力为T,重力加速度为g,则( )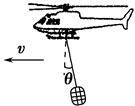
| A.f=mgsin θ | B.f=mgtan θ | C.T=mgcos θ | D.T= |