题目内容
 (2005?深圳一模)地球上空有人造地球同步通讯卫星,它们向地球发射微波.但无论同步卫星数目增到多少个,地球表面上总有一部分面积不能直接收到它们发射来的微波,请导出这个面积S与地球表面积S0之比的数学表达式;并根据提供的数据求出该比值至少为多大?
(2005?深圳一模)地球上空有人造地球同步通讯卫星,它们向地球发射微波.但无论同步卫星数目增到多少个,地球表面上总有一部分面积不能直接收到它们发射来的微波,请导出这个面积S与地球表面积S0之比的数学表达式;并根据提供的数据求出该比值至少为多大?(结果要求保留两位有效数字.已知地球半径R0=6.4×106m,地球表面的重力加速度g=10m/s2,半径为R高、为h的球缺的表面积为S1=2πRh,如图所示,球的表面积为S=4πR2)
分析:同步卫星总是在赤道上空,其高度也是一定的.由它画一条到地球表面的切线,可见两极周围的区域内就收不到微波通讯.
根据万有引力提供向心力和数学几何关系求解.
根据万有引力提供向心力和数学几何关系求解.
解答:解:(1)如图所示,因为同步卫星总是在赤道上空,其高度也是一定的.由它画一条到地球表面的切线,可见两极周围的区域内就收不到微波通讯.以m、M分别表示卫星和地球的质量,r表示卫星到地心的距离,T表示地球的自转周期,则对地球上质量为m0的
物体有G
=m0g,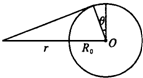
对地球同步卫星有G
=m(
)2r
又根据几何关系有rsinθ=R0
以S'表示某个极周围收不到微波区域的面积,则S′=2πR02(1-cosθ)
地球有两个极,因而接收不到微波区域的面积与地球表面积S0之比为:
=
=1-
(2)代入数据解得
=0.011
答:不能直接收到它们发射来的微波面积S与地球表面积S0之比的数学表达式是
=1-
,大小是0.011.
物体有G
| m0M |
| R02 |

对地球同步卫星有G
| mM |
| r2 |
| 2π |
| T |
又根据几何关系有rsinθ=R0
以S'表示某个极周围收不到微波区域的面积,则S′=2πR02(1-cosθ)
地球有两个极,因而接收不到微波区域的面积与地球表面积S0之比为:
| S |
| S0 |
| 2S′ |
| S0 |
1-(
|
(2)代入数据解得
| 2S′ |
| S0 |
答:不能直接收到它们发射来的微波面积S与地球表面积S0之比的数学表达式是
| S |
| S0 |
1-(
|
点评:解决该题关键要根据题意找出收不到微波区域的面积,善于把物理问题与数学几何图形结合运用.

练习册系列答案
相关题目
 (2005?深圳一模)如图所示,质量为m的子弹以速度v0水平击穿放在光滑水平地面上的木块.木块长L,质量为M,木块对子弹的阻力恒定不变,子弹穿过木块后木块获得动能为Ek.若木块或子弹的质量发生变化,但子弹仍穿过,则( )
(2005?深圳一模)如图所示,质量为m的子弹以速度v0水平击穿放在光滑水平地面上的木块.木块长L,质量为M,木块对子弹的阻力恒定不变,子弹穿过木块后木块获得动能为Ek.若木块或子弹的质量发生变化,但子弹仍穿过,则( ) (2005?深圳一模)在匀强磁场中有一个原来静止的碳14原子核,它放射出的粒子与反冲核的径迹是两个相内切的圆,如图所示.那么碳14的衰变方程为( )
(2005?深圳一模)在匀强磁场中有一个原来静止的碳14原子核,它放射出的粒子与反冲核的径迹是两个相内切的圆,如图所示.那么碳14的衰变方程为( ) (2005?深圳一模)如图所示,一个静电电势差计(简称静电计)放在绝缘面上,静电计的金属球A用导线经电键S1与其金属外壳B相接,又用导线经电键S2与大地相接.当S1与S2都断开时,使A球带电,看到静电计指针张开一个角度,现闭合电键S1后再断开,然后再闭合电键S2,可观察到的现象是( )
(2005?深圳一模)如图所示,一个静电电势差计(简称静电计)放在绝缘面上,静电计的金属球A用导线经电键S1与其金属外壳B相接,又用导线经电键S2与大地相接.当S1与S2都断开时,使A球带电,看到静电计指针张开一个角度,现闭合电键S1后再断开,然后再闭合电键S2,可观察到的现象是( )