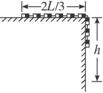
题目内容
如图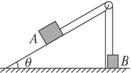
图
解析:连接体运动过程中两物体速度始终相等,绳断前连接体组成的系统机械能守恒,A机械能的减少量等于物块B机械能的增加量,列守恒方程.绳断后B的机械能守恒,以B为对象列机械能守恒方程,由两方程求解即可.
设细线断裂前一瞬间A和B速度的大小为v,A沿斜面下滑s的过程中,A的高度降低了ssinθ,B的高度升高了s.对A和B以及地球组成的系统,机械能守恒,有物块A机械能的减少量等于物块B机械能的增加量,即4mgssinθ-![]() ·4mv2=mgs+
·4mv2=mgs+![]() mv2
mv2
细线断后,物块B做竖直上抛运动,物块B与地球组成的系统机械能守恒,设物块B继续上升的高度为h,有mgh=![]() mv2
mv2
由以上两式联立解得h=![]()
故物块B上升的最大高度为H=s+h=s+![]() s.
s.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目