题目内容
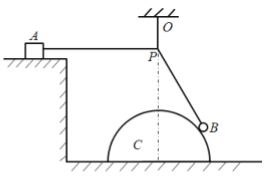
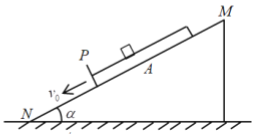
【题目】如图，一固定且足够长的斜面MN与水平面的夹角
，斜面上有一质量为3m、上表面光滑且下端有挡板P的长木板A沿斜面匀速向下运动，速度大小
，现将一质量为m的小滑块轻轻地放在长木板上，当小滑块运动到挡板P时（与挡板碰前的瞬间），长木板的速度刚好减为零，之后小滑块与挡板发生第1次碰撞，以后每隔一段时间，小滑块就与挡板碰撞一次，小滑块始终在长木板上运动，已知小滑块与挡板的碰撞为弹性碰撞且磁撞时间极短，重力加速度
，
，
，下列说法正确的是（ ）
A.小滑块在长木板上下滑过程中，长木板的加速度大小为
B.小滑块放在木板上的瞬间，其与P的距离为
C.小滑块与挡板第1次碰撞后的瞬间，小滑块的速度大小为1.5m/s
D.小滑块与挡板第2次碰撞后的瞬间，小滑块的速度大小为1.5m/s
【答案】CD
【解析】
A．长木板开始匀速下滑，由平衡条件得
解得
把小滑块放上长木板后，对长木板，由牛顿第二定律得
解得
故A错误；
BC．长木板上表面光滑，碰撞前小滑块做匀加速直线运动，小滑块加速运动时间
设小滑块与挡板第一次碰撞前小滑块的速度为v，则
滑块与挡板碰撞过程系统动量守恒，由动量守恒定律得
由机械能守恒定律得
解得
小滑块的位移为
木板的位移为
小滑块放在木板上的瞬间，其与P的距离为
故B错误，C正确；
D．碰撞后长木板速度再次减为零的时间
此时小滑块的速度为
解得
滑块与挡板碰撞过程系统动量守恒，由动量守恒定律得
由机械能守恒定律得
解得
故D正确。
故选CD。
练习册系列答案
相关题目
