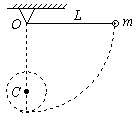
题目内容
长为L的轻绳，一端固定在O点，另一端拴一质量为m的小球，小球从最低点开始运动．若小球恰能在竖直平面内做圆周运动，取O点所在平面为零势能面，则小球在最低点时，具有的机械能为（ ）
| A、2mgL | ||
B、
| ||
C、
| ||
| D、mgL |
分析：小球恰能通过最高点，由牛顿第二定律求出在最高点的速度，在整个过程中只有重力做功，由机械能守恒可知，在最低点的机械能
解答：解：小球恰能通过最高点，由牛顿第二定律可知小球在最高点的速度
mg=
v=
取O点所在平面为零势能面，在整个运动过程中机械能守恒
最低点的机械能为：E=mgL+
mv2=mgL+
mgL=
mgL
故选：B
mg=
| mv2 |
| L |
v=
| gL |
取O点所在平面为零势能面，在整个运动过程中机械能守恒
最低点的机械能为：E=mgL+
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选：B
点评：通过圆周运动求出小球在最高点的速度，在整个过程中由机械能守恒可知，即可求的在最低点的机械能．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
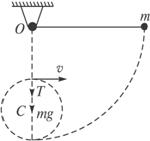
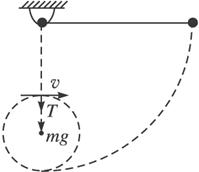
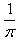，如图所示。欲使小球到达最低点后以C为圆心至少做一次完整的圆周运动，则h应满足什么条件？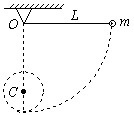
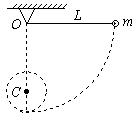，如图所示，(1) 欲使小球到达最低点后以C为
圆心至少做一次完整的圆周运动，则h应满足什么条件？
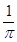，如图所示，(1) 欲使小球到达最低点后以C为圆心至少做一次完整的圆周运动，则h应满足什么条件？