Question

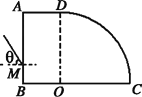
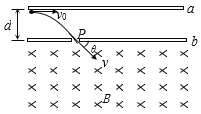
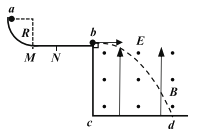
【题目】两个小球a、b质量均为2kg，b球置于水平台的右边缘，带q=0.2C正电荷；a球从半径R=0.8m的四分之一光滑圆弧轨道顶端，从静止开始滑下。与b发生完全非弹性碰撞后，一起飞入互相垂直的复合场中，已知水平台的MN段粗糙，且MN段长L=2m，摩擦因数μ=0.2，轨道Nb部分光滑。匀强电场竖直向上，匀强磁场水平向外。弧线bd是a、b一起在复合场中运动的轨迹，且bc=cd，E=200N/C，B=10T，取g=10m/s2。求：

(1)a下滑到圆弧轨道末端M点时，对轨道的压力大小

(2)水平台的高度

(3)a、b在复合场中运动的时间

(4)整个过程中a、b系统损失多少机械能

Answer 1

【答案】(1)60N，方向竖直向下 （2）m （3）3.14s (4)125J

【解析】

（1）根据机械能守恒定律求解a球到达M点的速度，根据牛顿第二定律求解a对圆弧轨道的压力；

（2）ab碰撞过程，动量守恒；在复合场中做匀速圆周运动，求解运动半径，从而求解水平台的高度；

（3）在复合场中运动的时间为；

（4）根据功能关系求解ab系统损失的机械能.

（1）a球从释放到圆弧最低点M时，机械能守恒：mgR=mvM2

解得vM=4m/s；

在M点，根据牛顿第二定律：N-mg=m

解得N=60N

根据牛顿第三定律可知，a对圆弧轨道的压力为N′=N=60N，方向竖直向下；

（2）a球从M到P由动能定理：

解得vP=2m/s

ab碰撞过程，由动量守恒定律：mvP=2mv

解得v=m/s

复合场中，因F电=qE=2mg=40N，所以做匀速圆周运动，

由qvB=2m可得：

水平台面的高度为h=r=2m

（3）在复合场中运动的时间为

（4）根据功能关系可知，ab系统损失的机械能为：

解得E损≈125J