题目内容

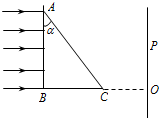如图所示，△ABC为一直角三棱镜的截面，其顶角α=30°，P为垂直于直线BCO的光屏，现有一宽度等于AB的单色平行光束垂直射向AB面，结果在屏P上形成一宽度等于
23
AB的光带，（AC面上折射的光都能入射到光屏P上）求棱镜的折射率．
分析：平行光束垂直射向AB面方向不变，在AC面发生折射，作出光路图．根据几何知识求出AC面上的入射角和折射角，再由折射定律求解折射率n．
解答：解：平行光束经棱镜折射后的出射光束仍是平行光束，如图所示．图中α、β为AC面上的入射角和折射角．
设出射光线与水平方向成θ角．
由几何关系得：tanθ=
1
3
AB
BC
=
1
3
AB
ABtanα
=
1
3tan30°
=
3
3
，得θ=30°，β=θ+α=60°
光线在AC面上折射，有n=
sinβ
sinα
=
3

答：棱镜的折射率是
3
．
点评：本题的解题关键是正确作出光路图，根据几何知识求解入射角和折射角，再运用折射定律求折射率．
练习册系列答案
相关题目
如图所示，ABC为等腰三棱镜，顶角A的角度为α，一条单色光线从AB边射入，进入三棱镜内的光线与底边BC平行，三棱镜的出射光线与入射光线的偏向角为β，求该三棱镜的折射率n．如α=60°，β=30°，那么n为多大？
如图所示，ABC为一细圆管构成的
34
圆轨道，将其固定在竖直平面内，轨道半径为R（比细圆管的半径大得多），OA水平，OC竖直，最低点为B，最高点为C，细圆管内壁光滑．在A点正上方某位置有一质量为m的小球（可视为质点）由静止开始下落，刚好进入细圆管内运动．已知细圆管的内径稍大于小球的直径，不计空气阻力．
（1）若小球经过C点时恰与管壁没有相互作用，求小球经过C点时的速度大小；
（2）若小球刚好能到达轨道的最高点C，求小球经过最低点B时的速度大小和轨道对小球的作用力大小；
（3）若小球从C点水平飞出后恰好能落回到A点，求小球刚开始下落时距离A点的高度．
（2013?厦门模拟）如图所示，ABC为某种透明介质的横截面图，其中△AOC为等腰直角三角形，BC为四分之一圆弧，AB与水平屏幕MN垂直并接触于A点．由红光和紫光两种单色光组成的复色光经过BC面射向圆心O，在AB分界面上的入射角i=45°，结果在水平屏幕MN上出现两个亮斑．则（　　）
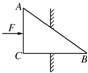精英家教网如图所示，同一竖直线的A、B两点固定有等量异种点电荷，电量为q，正负如图所示，△ABC为一等边三角形（边长为L），CD为AB边的中垂线，且与右侧竖直光滑
14
圆弧轨道的最低点C相切，已知圆弧的半径为R，现把质量为m带电量为+Q的小球（可视为质点）由圆弧的最高点M静止释放，到最低点C时速度为v0．已知静电力恒量为k，现取D为电势零点，求：
（1）在等量异种电荷A、B的电场中，M点的电势φM
（2）在最低点C轨道对小球的支持力FN多大？
精英家教网如图所示，ABC为一直角劈形物体，将其卡于孔中，劈的斜边AB=10cm，直角边AC=2cm．当用F=100N的力沿水平方向推劈时，求劈的AB面和BC面产生的推力各为多大？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网