题目内容
4．
如图所示，小船过河时，船头与上游河岸夹角为a，其航线恰好垂直于河岸，已知船在静水中的速度为z，现水流速度稍有增大，为保持航线不变，且能准时到达河对岸，下列措施中可行的是（ ）| A． | 减小a角，减小船速v | B． | 减小a角，增大船速v | ||
| C． | 增大a角，增大船速v | D． | 增大a角，减小船速v |
分析 将小船的运动分解为沿河岸方向和垂直于河岸方向，抓住分运动与合运动具有等时性，求出到达对岸沿水流方向上的位移以及时间．
当实际航线与河岸垂直，则合速度的方向垂直于河岸，根据平行四边形定则求出船头与河岸所成的夹角．
解答 
解：由题意可知，船相对水的速度为v，其航线恰好垂直于河岸，当水流速度稍有增大，为保持航线不变，且准时到达对岸，则如图所示，可知，故B正确，ACD错误；
故选：B．
点评 解决本题的关键知道分运动和合运动具有等时性，以及会根据平行四边形定则对运动进行合成和分解．
练习册系列答案
相关题目
13．
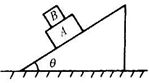两块叠放的长方体滑块A和B，置于固定的倾角为θ的斜面上，如图所示，滑块A和B的质量分别为M和m，A与斜面间的动摩擦因数为μ1，B与A之间的动摩擦因数为μ2，已知两滑块都从静止开始以相同的加速度从斜面滑下，则滑块B受到的摩擦力（ ）
两块叠放的长方体滑块A和B，置于固定的倾角为θ的斜面上，如图所示，滑块A和B的质量分别为M和m，A与斜面间的动摩擦因数为μ1，B与A之间的动摩擦因数为μ2，已知两滑块都从静止开始以相同的加速度从斜面滑下，则滑块B受到的摩擦力（ ）| A． | 等于零 | B． | 大小小于μ1mgcosθ | ||
| C． | 大小等于μ1mgcosθ | D． | 大小等于μ2mgcos |
15．如图是某物体做直线运动的速度图象，由图象可得到的正确结果是（ ）
| A． | t=1s时物体的加速度大小为1.0m/s2 | |
| B． | t=5s时物体的加速度大小为0.75m/s2 | |
| C． | 第3s内物体的位移为1.5m | |
| D． | 物体在加速过程的速度变化率比减速过程的速度变化率大 |
12．
如图所示，竖直平面内光滑圆轨道半径R=2m，从最低点A有一质量为m=1kg的小球开始运动，初速度v0方向水平向右，重力加速度g取10m/s2，下列说法正确的是（ ）
如图所示，竖直平面内光滑圆轨道半径R=2m，从最低点A有一质量为m=1kg的小球开始运动，初速度v0方向水平向右，重力加速度g取10m/s2，下列说法正确的是（ ）| A． | 小球能到达最高点B的条件是v0≥4$\sqrt{5}$m/s | |
| B． | 若初速度v0=5m/s，则运动过程中，小球一定不会脱离圆轨道 | |
| C． | 若初速度v0=8m/s，则小球将在离A点3.2m高的位置离开圆轨道 | |
| D． | 若初速度v0=8m/s，则小球离开圆轨道时的速度大小为2$\sqrt{2}$m/s |
19．甲 乙两车同时同地同向运动，甲车初速度为30m/s，以加速度大小为a1匀减速刹车，乙车初速度为10m/s，以加速度a2匀加速运动，经过时间t后两车速度共同速度为v．在乙车追上甲车之前两车之间最大距离为x．则（ ）
| A． | a1越大x越大 | B． | a2越小v越大 | C． | a1越大x越小 | D． | a2越大t越小 |
9．在距水平地面不同高度以相同的水平初速度分别抛出甲、乙两物体，若两物体由抛出点到落地点的水平距离之比为3：1，则甲、乙两物体抛出点到地面的高度之比为（ ）
| A． | $\sqrt{3}$：1 | B． | 2：1 | C． | 3：1 | D． | 9：1 |
16．下列说法正确的是（ ）
| A． | 各种机械铭牌上所标的功率一般是额定功率 | |
| B． | 功率是标量，大小等于力和速度大小的乘积 | |
| C． | 力做功越多，力的功率就越大 | |
| D． | 汽车以一恒定的加速度从静止开始做匀加速运动的最长时间为t，此后开始以最大速度匀速运动 |
13．一个电子穿过某一空间而未发生偏转，则此空间下列说法不正确的是（ ）
| A． | 一定不存在磁场 | B． | 可能只存在电场 | ||
| C． | 可能存在方向重合的电场和磁场 | D． | 可能存在正交的磁场和电场 |
如图所示，质量为m的带负电的小物块置于倾角为37°的光滑斜面上，当整个装置处于竖直向下的匀强电场中时，小物块恰好静止在斜面上．现将电场方向突然改为水平向右，而场强大小不变，问：小物块将沿斜面如何运动？