题目内容
2.我国向月球发射一颗绕月探测卫星“嫦娥一号”,“嫦娥一号”进入月球轨道后,在距离月球表面高为h的轨道上绕月球做匀速圆周运动.已知月球半径为R月,月球表面的重力加速度为g月,万有引力常量为G.(1)月球质量表达式;
(2)“嫦娥一号”环绕月球运行的周期;
(3)若地球半径为R地,地球表面的重力加速度为g地,且有R月=$\frac{{R}_{地}}{4}$,g月=$\frac{{g}_{地}}{6}$,则近月卫星的运行速度与近地卫星运行速度的比值约为多少?
分析 (1)根据万有引力等于重力,求出月球质量的表达式;
(2)根据万有引力提供向心力,求出“嫦娥一号”环绕月球运行的周期;
(3)根据重力提供向心力得出速度的表达式,结合半径和重力加速度之比求出近月卫星的运行速度与近地卫星运行速度的比值.
解答 解:(1)根据$G\frac{Mm}{{{R}_{月}}^{2}}=m{g}_{月}$得,月球的质量M=$\frac{{g}_{月}{{R}_{月}}^{2}}{G}$.
(2)根据$G\frac{Mm}{({R}_{月}+h)^{2}}=m({R}_{月}+h)\frac{4{π}^{2}}{{T}^{2}}$得,T=$\sqrt{\frac{4{π}^{2}({R}_{月}+h)^{3}}{GM}}$,
又GM=$g{{R}_{月}}^{2}$,
解得T=$\sqrt{\frac{4{π}^{2}({R}_{月}+h)^{3}}{g{{R}_{月}}^{2}}}$.
(3)根据mg=m$\frac{{v}^{2}}{R}$得,v=$\sqrt{gR}$,
因为$\frac{{R}_{月}}{{R}_{地}}=\frac{1}{4}$,$\frac{{g}_{月}}{{g}_{地}}=\frac{1}{6}$,
则$\frac{{v}_{1}}{{v}_{2}}=\sqrt{\frac{1}{24}}$=0.2.
答:(1)月球质量表达式为M=$\frac{{g}_{月}{{R}_{月}}^{2}}{G}$;
(2)“嫦娥一号”环绕月球运行的周期为$\sqrt{\frac{4{π}^{2}({R}_{月}+h)^{3}}{g{{R}_{月}}^{2}}}$.
(3)近月卫星的运行速度与近地卫星运行速度的比值约为0.2.
点评 解决本题的关键掌握万有引力定律的两个重要推论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| A. | vA=5m/s,vB=2.5m/s | B. | vA=2m/s,vB=4m/s | ||
| C. | vA=-4m/s,vB=7m/s | D. | vA=7m/s,vB=1.5m/s |
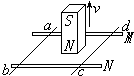 如图所示,固定在水平面上的两平行光滑的金属导轨M、N,垂直放着两可滑动的导线ab、cd,在导线框内,竖直放置一条形磁铁,当条形磁铁迅速上抽的过程中,则导线ab、cd将( )
如图所示,固定在水平面上的两平行光滑的金属导轨M、N,垂直放着两可滑动的导线ab、cd,在导线框内,竖直放置一条形磁铁,当条形磁铁迅速上抽的过程中,则导线ab、cd将( )| A. | 保持静止 | B. | 相互靠近 | C. | 相互远离 | D. | 先靠近后远离 |
 甲、乙两车在同一水平路面上的两平行车道做直线运动,某时刻乙车在前、甲车在后,相距6m,从此刻开始计时,两车运动的v-t图象如图所示,在0一8s内,下列说法正确的是( )
甲、乙两车在同一水平路面上的两平行车道做直线运动,某时刻乙车在前、甲车在后,相距6m,从此刻开始计时,两车运动的v-t图象如图所示,在0一8s内,下列说法正确的是( )| A. | t=4s时两车相距2m | B. | t=4s时两车相遇 | ||
| C. | t=8s时两车相遇 | D. | 开始时两车相距最远 |
| A. | 航天器轨道高度降低后,向心加速度减小 | |
| B. | 航天器轨道高度降低后,飞行速度减小 | |
| C. | 航天器轨道高度降低过程中,飞行周期变小 | |
| D. | 要使航天器再次回到预定轨道,可以通过航天器发动机点火加速实现 |
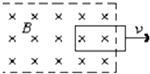 如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界匀强磁场区域,v1=2v2.在先后两种情况下( )
如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界匀强磁场区域,v1=2v2.在先后两种情况下( )| A. | 线圈中的感应电流之比为I1:I2=1:2 | |
| B. | 线圈中的感应电流之比为I1:I2=2:1 | |
| C. | 通过线圈某截面的电荷量之比q1:q2=1:2 | |
| D. | 通过线圈某截面的电荷量之比q1:q2=2:1 |
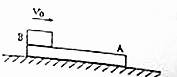 如图所示,质量为M的长木板A静止放在光滑的水平地面上,质量为m的物体B以水平速度v0冲上A,由于摩擦力作用,最后停止在木板A上.若从B冲到木板A上到相对木板A静止的过程中,木板A的动能增加了12J,并且M>m.则此过程中产生的内能可能是( )
如图所示,质量为M的长木板A静止放在光滑的水平地面上,质量为m的物体B以水平速度v0冲上A,由于摩擦力作用,最后停止在木板A上.若从B冲到木板A上到相对木板A静止的过程中,木板A的动能增加了12J,并且M>m.则此过程中产生的内能可能是( ) 如图所示,实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.05s时刻的波形图.则:
如图所示,实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.05s时刻的波形图.则: