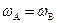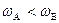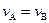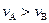题目内容
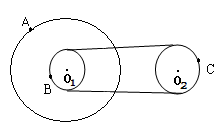
如图，主动轮O1上两轮的半径分别为3r和r，从动轮O2的半径为2r，A、B、C分别为轮缘上的三点，设皮带不打滑，求A、B、C三点的角速度和线速度之比：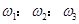 
= .
= .
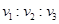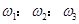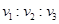= .= .2：2：1 ， 3：1：1 .
考点：
专题：匀速圆周运动专题．
分析：靠传送带传动的点，线速度大小相等，共轴的点，角速度相等．B点和C点具有相同的线速度，A点和B点具有相同的角速度．根据v=rω，求出三点的角速度之比，线速度之比．
解答：解：B点和C点具有相同的线速度，根据ω=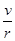
，知B、C两点的角速度之比等于半径之反比，所以ωB：ωC=rc：rb=2：1．而A点和B点具有相同的角速度，所以ωA：ωB：ωC=2：2：1．．
根据v=rω，知A、B的线速度之比等于半径之比，所以vA：vB：=3：1．B、C线速度相等，所以vA：vB：vC=3：1：1．
故本题答案为：2：2：1，3：1：1．
点评：解决本题的关键掌握靠传送带传动的点，线速度大小相等，共轴的点，角速度相等．
专题：匀速圆周运动专题．
分析：靠传送带传动的点，线速度大小相等，共轴的点，角速度相等．B点和C点具有相同的线速度，A点和B点具有相同的角速度．根据v=rω，求出三点的角速度之比，线速度之比．
解答：解：B点和C点具有相同的线速度，根据ω=
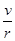，知B、C两点的角速度之比等于半径之反比，所以ωB：ωC=rc：rb=2：1．而A点和B点具有相同的角速度，所以ωA：ωB：ωC=2：2：1．．根据v=rω，知A、B的线速度之比等于半径之比，所以vA：vB：=3：1．B、C线速度相等，所以vA：vB：vC=3：1：1．
故本题答案为：2：2：1，3：1：1．
点评：解决本题的关键掌握靠传送带传动的点，线速度大小相等，共轴的点，角速度相等．
练习册系列答案
相关题目
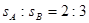，半径转过的角度之比
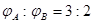，则它们的线速度之比
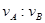= ，周期之比
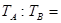，半径之比
。
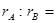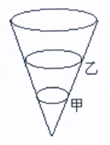
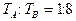，则轨道半径之比和运动速率之比分别为（）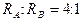
，
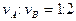
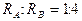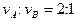
下端连接一只小球，小球与
地面间的距离可以忽略（但小球不受地面支持力）且处于静止状态．现给小球一沿水平方向的初速度，使其开始在竖直平面内做圆周运动。设小球到达最高点时轻绳突然断开，已知最后小球落在距
初
始位置水平距离为4R
、
，
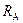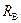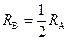．设A、B两点的角速度大小分别为
、
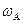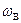，线速度的大小分别为
、
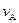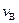．则下列关系正确的是
