题目内容
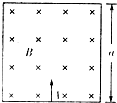
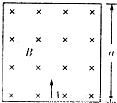
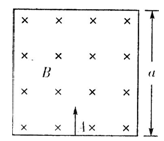
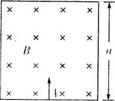
如图所示,光滑绝缘壁围成的正方形匀强磁场区域,边长为a磁场的方向垂直于正方形平面向里,磁感应强度的大小为B.有一个质量为m、电量为q的带正电的粒子,从下边界正中央的A孔垂直于下边界射入磁场中.设粒子与绝缘壁碰撞时无能量和电量损失,不计重力和碰撞时间.
(1)若粒子在磁场中运动的半径等于a/2,则粒子射入磁场的速度为多大?经多长时间粒子又从A孔射出?
(2)若粒子在磁场中运动的半径等于a/4,判断粒子能否再从A孔射出.如能,求出经多长时间粒子从A孔射出;如不能,说出理由.
(3)若粒子在磁场中运动的半径小于a且仍能从A孔垂直边界射出,粒子射入的速度应为多大?在磁场中的运动时问是多长?
分析:(1)若粒子在磁场中运动的半径等于a/2,则粒子粒子在磁场中运动4个
圆后从A点射出,所以可以知道粒子运动的半径,然后由洛伦兹力提供向心力去粒子的速度和运动的时间;
(2)若粒子在磁场中运动的半径等于a/4,则粒子在运动半个圆周后与绝缘壁碰撞然后做匀速直线运动,在另一侧与绝缘壁碰撞后做匀速圆周运动,两个半圆后做匀速直线运动…直到出来;
(3)给定的条件下的粒子的运动轨迹如图.代人公式即可讨论.
解答:解:带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,得:
qvB=又:
r=整理得:
v=由:
T=得:
T=粒子在磁场中运动4个
圆后从A点射出,所以:
t=T=(2)能.粒子运动的轨迹如图,
由
qvB=,
r=得:
v=t=+2=m(3)第一种情景:
r1==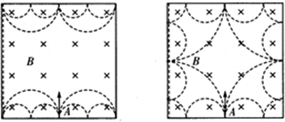 v1=,其中n=1、2、3…t1=+2nT=
v1=,其中n=1、2、3…t1=+2nT=,其中n=1、2、3…
第二种情景:
r2==v2=,其中n=1、2、3…t2=(4n+1)T=,其中n=1、2、3…
答:(1)若粒子在磁场中运动的半径等于a/2,则粒子射入磁场的速度为
v=,经时间
粒子又从A孔射出;
(2)若粒子在磁场中运动的半径等于a/4,粒子能再从A孔射出.经时间
m粒子从A孔射出;
(3)若粒子在磁场中运动的半径小于a且仍能从A孔垂直边界射出,粒子射入的速度以及在磁场中的运动时间有两种情况:
第一种情景:
r1==v1=,其中n=1、2、3…t1=+2nT=,其中n=1、2、3…
第二种情景:
r2==v2=,其中n=1、2、3…t2=(4n+1)T=,其中n=1、2、3…
点评:在带电粒子在磁场中的运动中,正确画出粒子的运动轨迹是解题的关键.尤其是情景比较复杂的情况下,更是如此.题目的难度较大.
练习册系列答案
相关题目
 如图所示,光滑绝缘壁围成的正方形匀强磁场区域,边长为a磁场的方向垂直于正方形平面向里,磁感应强度的大小为B.有一个质量为m、电量为q的带正电的粒子,从下边界正中央的A孔垂直于下边界射入磁场中.设粒子与绝缘壁碰撞时无能量和电量损失,不计重力和碰撞时间.
如图所示,光滑绝缘壁围成的正方形匀强磁场区域,边长为a磁场的方向垂直于正方形平面向里,磁感应强度的大小为B.有一个质量为m、电量为q的带正电的粒子,从下边界正中央的A孔垂直于下边界射入磁场中.设粒子与绝缘壁碰撞时无能量和电量损失,不计重力和碰撞时间.


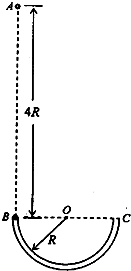 如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直平面内,管口B、C的连线是水平直径.现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R.从小球进入管口开始,整个空间突然加上一个匀强电场,电场力在竖直向上的分力大小与重力大小相等,结果小球从管口C处脱离圆管后,其运动轨迹最后经过A点.设小球运动过程中带电量没有改变,重力加速度为g.求:
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直平面内,管口B、C的连线是水平直径.现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R.从小球进入管口开始,整个空间突然加上一个匀强电场,电场力在竖直向上的分力大小与重力大小相等,结果小球从管口C处脱离圆管后,其运动轨迹最后经过A点.设小球运动过程中带电量没有改变,重力加速度为g.求: