题目内容
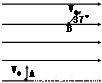
 如图所示,有一水平向左的匀强电场,场强为E=1.25×104 N/C,一根长L=1.5m、与水平方向的夹角为θ=37°的光滑绝缘细直杆MN固定在电场中,杆的下端M固定一个带电小球A,电荷量Q=+4.5×10-6 C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6 C,质量m=1.0×10-2 kg.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×109 N?m2/C2,取g=10m/s2,sin 37°=0.6,cos 37°=0.8)求:
如图所示,有一水平向左的匀强电场,场强为E=1.25×104 N/C,一根长L=1.5m、与水平方向的夹角为θ=37°的光滑绝缘细直杆MN固定在电场中,杆的下端M固定一个带电小球A,电荷量Q=+4.5×10-6 C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6 C,质量m=1.0×10-2 kg.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×109 N?m2/C2,取g=10m/s2,sin 37°=0.6,cos 37°=0.8)求:(1)小球B开始运动时的加速度为多大?
(2)小球B的速度最大时,与M端的距离r为多大?
分析:(1)分析小球B的受力情况,根据牛顿第二定律和库仑定律求解小球B开始运动时的加速度.
(2)当小球所受的合外力为零时速度最大,由上题结果求解.
(2)当小球所受的合外力为零时速度最大,由上题结果求解.
解答:解:(1)开始运动时小球B受重力、库仑力、杆的弹力和电场力,沿杆方向运动,由牛顿第二定律得:
mgsinθ-
-qEcosθ=ma ①
解得:a=gsinθ-
-
②
代入数据解得:
a=(10×0.6-
-
)m/s2=3.2m/s2③
(2)小球B速度最大时合力为零,即
mgsinθ-
-qEcosθ=0 ④
解得:r=
⑤
代入数据解得:r=
m=0.9m
答:(1)小球B开始运动时的加速度为3.2m/s2.(2)小球B的速度最大时,与M端的距离r为0.9m.
mgsinθ-
| kQq |
| L2 |
解得:a=gsinθ-
| kQq |
| mL2 |
| qEcosθ |
| m |
代入数据解得:
a=(10×0.6-
| 9.0×109×(+4.5×10-6)×(+1.0×10-6) |
| 1.0×10-2×1.52 |
| (+1.0×10-6)×1.25×104×0.8 |
| 1.0×10-2 |
(2)小球B速度最大时合力为零,即
mgsinθ-
| kQq |
| r2 |
解得:r=
|
代入数据解得:r=
|
答:(1)小球B开始运动时的加速度为3.2m/s2.(2)小球B的速度最大时,与M端的距离r为0.9m.
点评:解答本题关键是能够正确对小球B进行受力分析和运动分析,运用牛顿第二定律求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
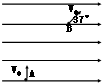 如图所示,有一水平向右的匀强电场,一个质量为m、电荷量为+q的小球以初速度V0从A点竖直向上射入电场中,小球通过电场中B点时速度的大小仍为V0,方向与电场方向成37°斜向上,则A、B两点的电势差为( )
如图所示,有一水平向右的匀强电场,一个质量为m、电荷量为+q的小球以初速度V0从A点竖直向上射入电场中,小球通过电场中B点时速度的大小仍为V0,方向与电场方向成37°斜向上,则A、B两点的电势差为( ) 如图所示,有一水平向右的匀强电场,场强为E=1.25×104 N/C,一根长L=1.5m、与水平方向的夹角为θ=37°的光滑绝缘细直杆MN固定在电场中,杆的下端M固定一个带电小球A,电荷量Q=+4.5×10-6 C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6 C,质量m=1.0×10-2 kg.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×109 N?m2/C2,取g=10m/s2,sin 37°=0.6,cos 37°=0.8)求:
如图所示,有一水平向右的匀强电场,场强为E=1.25×104 N/C,一根长L=1.5m、与水平方向的夹角为θ=37°的光滑绝缘细直杆MN固定在电场中,杆的下端M固定一个带电小球A,电荷量Q=+4.5×10-6 C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6 C,质量m=1.0×10-2 kg.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×109 N?m2/C2,取g=10m/s2,sin 37°=0.6,cos 37°=0.8)求: