题目内容
13. 如图所示,带有光滑的半径为R的$\frac{1}{4}$圆弧轨道的滑块静止在光滑水平面上,滑块的质量为M,使一个质量为m的小球由静止从A处释放,当小球从B点水平飞出时,滑块的速度为多大?
如图所示,带有光滑的半径为R的$\frac{1}{4}$圆弧轨道的滑块静止在光滑水平面上,滑块的质量为M,使一个质量为m的小球由静止从A处释放,当小球从B点水平飞出时,滑块的速度为多大?
分析 滑块与圆弧轨道水平方向不受外力,系统动量守恒;系统中只有重力势能向动能转化,机械能守恒;根据守恒定律列方程后联立求解.
解答 解:圆弧轨道与滑块组成的系统在水平方向动量守恒,以水平向右为正方向,在水平方向,由动量守恒定律得:
mv-Mv′=0,
对系统,由机械能守恒定律得:mgR=$\frac{1}{2}$mv2+$\frac{1}{2}$Mv′2,
解得:v′=$\frac{m}{M}$$\sqrt{\frac{2MgR}{M+m}}$;
答:当小球从B点水平飞出时,滑块的速度为$\frac{m}{M}$$\sqrt{\frac{2MgR}{M+m}}$.
点评 本题关键是明确滑块和轨道系统动量守恒、机械能也守恒,然后根据守恒定律列方程联立求解,解题时要注意系统整体动量不守恒,但水平方向动量守恒.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 如图所示,不带电的枕形导体的A、B两端各贴有一对金箔.当枕形导体的A端靠近一带电导体C时( )
如图所示,不带电的枕形导体的A、B两端各贴有一对金箔.当枕形导体的A端靠近一带电导体C时( )
 如图所示,不带电的枕形导体的A、B两端各贴有一对金箔.当枕形导体的A端靠近一带电导体C时( )
如图所示,不带电的枕形导体的A、B两端各贴有一对金箔.当枕形导体的A端靠近一带电导体C时( )| A. | A端金箔张开,B端金箔闭合 | |
| B. | 用手接触枕形导体,A端金箔张开,B端金箔闭合 | |
| C. | 用手接触枕形导体,后将手和C分别移走,两对金箔均张开 | |
| D. | 选项C中两对金箔带同种电荷 |
7.骑自行车的人沿着直线从静止开始运动,运动后,在第1s、第2s、第3s、第4s内,通过的路程分别为1m、2m、3m、4m,有关其运动的描述正确的是:( )
| A. | 前4s内的平均速度是2.5m/s | B. | 在第3、4s内平均速度是3.5m/s | ||
| C. | 第3s末的瞬时速度一定是3m/s | D. | 第2s内的平均速度是1m/s. |
5. 霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数),将传感器固定在物体上,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当物体沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向的上、下表面的电势差U也不同.则( )
霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数),将传感器固定在物体上,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当物体沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向的上、下表面的电势差U也不同.则( )
 霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数),将传感器固定在物体上,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当物体沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向的上、下表面的电势差U也不同.则( )
霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数),将传感器固定在物体上,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当物体沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向的上、下表面的电势差U也不同.则( )| A. | 若图中霍尔元件是电子导电,则上板电势比下板的电势低 | |
| B. | 电流I取值越大,上、下表面的电势差U越小 | |
| C. | 磁感强度B越大,上、下表面的电势差U越大 | |
| D. | k越大,传感器灵敏度($\frac{△U}{△z}$)越高 |
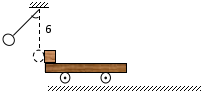 如图所示,质量为M的平板车P高h,质量为m的小物块Q的大小不计,位于平板车的左端,系统原来静止在光滑水平地面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系一质量也为m的小球(大小不计).今将小球拉至悬线与竖直位置成60°由静止释放,小球到达最低点时与Q的碰撞时间极短,且无机械能损失.Q与P之间的动摩擦因数为μ,平板车与Q的质量关系是M:m=4:1,重力加速度为g.为使小物块Q不滑离长木板,长木板至少多长?
如图所示,质量为M的平板车P高h,质量为m的小物块Q的大小不计,位于平板车的左端,系统原来静止在光滑水平地面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系一质量也为m的小球(大小不计).今将小球拉至悬线与竖直位置成60°由静止释放,小球到达最低点时与Q的碰撞时间极短,且无机械能损失.Q与P之间的动摩擦因数为μ,平板车与Q的质量关系是M:m=4:1,重力加速度为g.为使小物块Q不滑离长木板,长木板至少多长?