题目内容
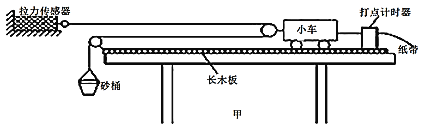
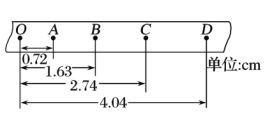
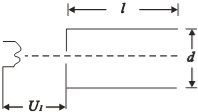
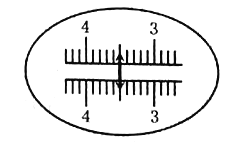
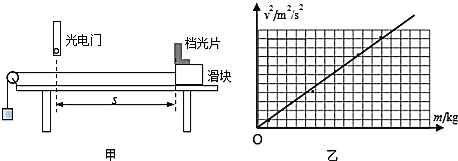
【题目】在研究“加速度与力的关系”实验中,某同学根据学过的理论设计了如下装置(如图甲):水平桌面上放置了气垫导轨,装有挡光片的滑块放在气垫导轨的某处(档光片左端与滑块左端齐平)。实验中测出了滑块释放点到光电门(固定)的距离为s,挡光片经过光电门的速度为v,钩码的质量为m,(重力加速度为g,摩擦可忽略)
(1)本实验中钩码的质量要满足的条件是__;
(2)该同学作出了v2—m的关系图象(如图乙),发现是一条过原点的直线,间接验证了“加速度与力的关系”,依据图象,每次小车的释放点有无改变__ (选填“有”或“无”),从该图象还可以求得的物理量是__。
【答案】钩码质量远小于滑块质量 无 滑块质量
【解析】
(1)![]() 设钩码质量为m,滑块质量为M,对整体分析,根据牛顿第二定律,滑块的加速度
设钩码质量为m,滑块质量为M,对整体分析,根据牛顿第二定律,滑块的加速度
a=![]()
隔离对滑块分析,可知细绳上的拉力
FT=Ma=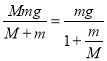
![]()
要保证绳子的拉力FT等于钩码的重力mg,则钩码的质量m要远小于滑块的质量M,这时有FT![]() ;
;
(2)![]() 滑块的加速度a=
滑块的加速度a=![]() ,当s不变时,可知加速度与v2成正比,滑块的合力可以认为等于钩码的重力,滑块的合力正比于钩码的质量,所以可通过v2﹣m的关系可以间接验证加速度与力的关系,在该实验中,s不变,v2—m的关系图象是一条过原点的直线,所以每次小车的释放点无改变;
,当s不变时,可知加速度与v2成正比,滑块的合力可以认为等于钩码的重力,滑块的合力正比于钩码的质量,所以可通过v2﹣m的关系可以间接验证加速度与力的关系,在该实验中,s不变,v2—m的关系图象是一条过原点的直线,所以每次小车的释放点无改变;
![]() 因为a与F成正比,则有:
因为a与F成正比,则有:![]() ,则
,则![]() ,结合图线的斜率可以求出滑块的质量M。
,结合图线的斜率可以求出滑块的质量M。

练习册系列答案
相关题目