题目内容
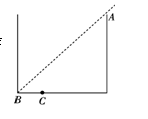
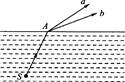
图示为一个储油圆柱桶,其底面直径与桶高相等.当桶中无油时,贴着桶的上边缘上的A点恰能看到桶底边缘上的B处;当桶内油的深度等于桶高的一半时,眼所处的位置不变,在桶外沿AB方向看去,恰能看到桶底上的C点,且BC的距离是桶底直径的四分之一(A、B、C三点在同一竖直平面内且BC在同一条直径线上).据此可估算出该油的折射率n和光在这种油中的传播速度v分别为(已知真空中的光速c=3×108 m/s)( )
A. 1.6、1.6×108 m/s B. 2.2、2.2×108 m/s
C. 2.0、1.6×108 m/s D. 1.6、1.9×108 m/s

A. 1.6、1.6×108 m/s B. 2.2、2.2×108 m/s
C. 2.0、1.6×108 m/s D. 1.6、1.9×108 m/s
D
光路如图(c)所示.
 由题意知,底面直径与桶高相等,所以图中角r=450 , 角i
由题意知,底面直径与桶高相等,所以图中角r=450 , 角i
可以计算出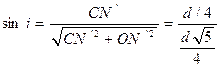 所以油的折射率n
所以油的折射率n
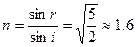
由于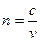
所以光在油中的速度 ,D对;
,D对;
 由题意知,底面直径与桶高相等,所以图中角r=450 , 角i
由题意知,底面直径与桶高相等,所以图中角r=450 , 角i可以计算出
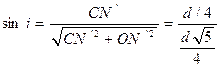 所以油的折射率n
所以油的折射率n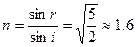
由于
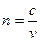
所以光在油中的速度
 ,D对;
,D对;
练习册系列答案
相关题目

 ,圆心角∠AOB=60°,一细束激光平行于角平分线由OA面的P点射入,射入介质后第一次射到界面上的N
,圆心角∠AOB=60°,一细束激光平行于角平分线由OA面的P点射入,射入介质后第一次射到界面上的N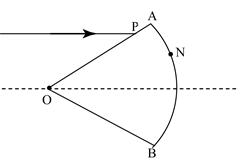
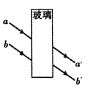
 m的单色光,以45o的入射角从空气射向折射率为
m的单色光,以45o的入射角从空气射向折射率为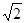 的某种玻璃中.求:
的某种玻璃中.求:
