题目内容
16.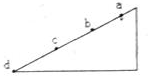 如图所示,一小球分别从光滑斜面上a、b、c三点由静止释放,到达底端d点需要的时间分别为t1、t2、t3,位移分别为x1、x2、x3,则下列关系正确的是( )
如图所示,一小球分别从光滑斜面上a、b、c三点由静止释放,到达底端d点需要的时间分别为t1、t2、t3,位移分别为x1、x2、x3,则下列关系正确的是( )| A. | $\frac{{x}_{1}}{{t}_{1}}>\frac{{x}_{2}}{{t}_{2}}>\frac{{x}_{3}}{{t}_{3}}$ | B. | $\frac{{x}_{1}}{{t}_{1}}=\frac{{x}_{2}}{{t}_{2}}=\frac{{x}_{3}}{{t}_{3}}$ | ||
| C. | $\frac{{x}_{1}}{{t}_{1}^{2}}>\frac{{x}_{2}}{{t}_{2}^{2}}>\frac{{x}_{3}}{{t}_{3}^{2}}$ | D. | $\frac{{x}_{1}}{{t}_{1}^{2}}=\frac{{x}_{2}}{{t}_{2}^{2}}=\frac{{x}_{3}}{{t}_{3}^{2}}$ |
分析 小球在光滑斜面上释放时均做加速度大小为gsinθ的匀加速运动,分别由位移公式x=$\frac{1}{2}a{t}^{2}$和平均速度公式求解x1、x2、x3与t1、t2、t3的关系.
解答 解:A、某段时间内的平均速度$\overline{v}=\frac{x}{t}=\frac{v}{2}$,因为三个小球到达底端的速度v1>v2>v3,根据$\overline{v}=\frac{v}{2}$,可知平均速度$\overline{{v}_{1}}>\overline{{v}_{2}}>\overline{{v}_{3}}$,所以$\frac{{x}_{1}}{{t}_{1}}$>$\frac{{x}_{2}}{{t}_{2}}$>$\frac{{x}_{3}}{{t}_{3}}$,故A正确,B错误;
C、小球在光滑斜面上释放时均做加速度大小为gsinθ的匀加速直线运动,加速度相同,由位移公式x=$\frac{1}{2}a{t}^{2}$得$\frac{{x}_{1}}{{{t}_{1}}^{2}}=\frac{{x}_{2}}{{{t}_{2}}^{2}}=\frac{{x}_{3}}{{{t}_{3}}^{2}}$,故D错误,C正确.
故选:AD.
点评 本题考查了运动学公式和推论的基本运用,掌握匀变速直线运动的位移时间公式和平均速度推论是解决本题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
6.关于磁电式电流表的说法,以下选项中正确的是( )
①指针稳定后,线圈受到螺旋弹簧的力矩与线圈受到的磁力矩方向是相反的
②通电线圈中的电流越大,电流表指针偏转的角度也越大
③在线圈转动的范围内,各处的磁场都是匀强磁场
④在线圈转动的范围内,线圈所受磁力大小与电流大小有关,而与所处位置无关.
①指针稳定后,线圈受到螺旋弹簧的力矩与线圈受到的磁力矩方向是相反的
②通电线圈中的电流越大,电流表指针偏转的角度也越大
③在线圈转动的范围内,各处的磁场都是匀强磁场
④在线圈转动的范围内,线圈所受磁力大小与电流大小有关,而与所处位置无关.
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ①②③④ |
7.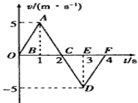 若一质点从t=0开始由原点出发沿直线运动,其速度-时间图象如图所示,则该质点( )
若一质点从t=0开始由原点出发沿直线运动,其速度-时间图象如图所示,则该质点( )
 若一质点从t=0开始由原点出发沿直线运动,其速度-时间图象如图所示,则该质点( )
若一质点从t=0开始由原点出发沿直线运动,其速度-时间图象如图所示,则该质点( )| A. | t=1s物体速度方向发生改变 | B. | t=2s时离原点最远 | ||
| C. | t=4s时回到原点,路程为10 m | D. | 物体一直沿着某一方向运动 |
11.一物体的位移随时间变化的关系式为x=3t+2t2,则下列说法正确的是( )
| A. | 物体的加速度为1m/s2 | |
| B. | 物体的加速度为4m/s2 | |
| C. | 第2s内物体的位移为14m | |
| D. | 物体的速度随时间变化的关系式为v=3+2t |
8.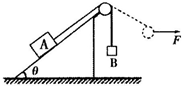 如图所示,斜面体放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,系统处于静止状态,现对B施加一水平力F使B缓慢地运动,使绳子偏离竖直方向一个角度(A与斜面体均保持静止),在此过程中( )
如图所示,斜面体放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,系统处于静止状态,现对B施加一水平力F使B缓慢地运动,使绳子偏离竖直方向一个角度(A与斜面体均保持静止),在此过程中( )
 如图所示,斜面体放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,系统处于静止状态,现对B施加一水平力F使B缓慢地运动,使绳子偏离竖直方向一个角度(A与斜面体均保持静止),在此过程中( )
如图所示,斜面体放置于粗糙水平地面上,物块A通过跨过光滑定滑轮的轻质细绳与物块B连接,系统处于静止状态,现对B施加一水平力F使B缓慢地运动,使绳子偏离竖直方向一个角度(A与斜面体均保持静止),在此过程中( )| A. | 水平力F一定增大 | B. | 斜面对物块A的摩擦力一定增大 | ||
| C. | 地面对斜面的摩擦力一定增大 | D. | 地面对斜面的支持力一定不变 |
5.已知三个力的合力为零,则这三个力的大小可能是( )
| A. | 15N,5N,6N | B. | 3N,6N,4N | C. | 1N,2N,10N | D. | 100N,100N,3N |
6.试判断下列的几个速度中哪个是瞬时速度( )
| A. | 子弹以800m/s的速度击中目标 | |
| B. | 汽车从甲站到乙站的速度是25m/s | |
| C. | 小球第3s内的速度是6m/s | |
| D. | 由于堵车,车在隧道内的速度仅为1.2m/s |
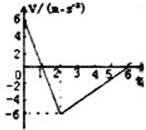 质点做直线运动的v-t图象如图所示,则该质点前6s的位移为-12m,4秒末的加速度为1.5m/s2.
质点做直线运动的v-t图象如图所示,则该质点前6s的位移为-12m,4秒末的加速度为1.5m/s2.