题目内容
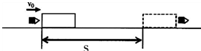 质量为M的木块在光滑水平面上处于静止状态,有一质量为m的子弹以水平速度v0击中木块并穿出,子弹穿出的速度是v1,子弹受到的阻力恒为f,则
质量为M的木块在光滑水平面上处于静止状态,有一质量为m的子弹以水平速度v0击中木块并穿出,子弹穿出的速度是v1,子弹受到的阻力恒为f,则(1)子弹射入并穿出木块的过程中木块在水平面上滑行的距离为多少?
(2)要使子弹恰好不穿出,木块的长度应为多少?
分析:1、子弹和木块构成一系统,在水平方向上动量守恒列出等式,子弹射入并穿出木块的过程中对木块运用动能定理列出等式求解.
2、子弹恰不射出,子弹和木块的速度相同,根据动量守恒和能量守恒求解.
2、子弹恰不射出,子弹和木块的速度相同,根据动量守恒和能量守恒求解.
解答:解:(1)子弹和木块构成一系统,在水平方向上合外力为零,在水平方向上动量守恒,
设子弹穿出木块瞬间木块的速度为v2
m0v0=mv1+Mv2 …①
木块在水平面上滑行的距离为S,子弹射入并穿出木块的过程中对木块运用动能定理得:
fS=
M
…②
联立①②解得:S=
(2)子弹恰不射出,在水平方向合外力为零,在水平方向上动量守恒.设子弹和木块的共同速度为v3
m0v0=(m0+M)v3
对整个过程,由能量守恒得:fL=
m
-
(M+m)
解得:L=
答:(1)子弹射入并穿出木块的过程中木块在水平面上滑行的距离为
(2)要使子弹恰好不穿出,木块的长度应为
.
设子弹穿出木块瞬间木块的速度为v2
m0v0=mv1+Mv2 …①
木块在水平面上滑行的距离为S,子弹射入并穿出木块的过程中对木块运用动能定理得:
fS=
| 1 |
| 2 |
| v | 2 2 |
联立①②解得:S=
| m2(v0-v1)2 |
| 2Mf |
(2)子弹恰不射出,在水平方向合外力为零,在水平方向上动量守恒.设子弹和木块的共同速度为v3
m0v0=(m0+M)v3
对整个过程,由能量守恒得:fL=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 3 3 |
解得:L=
M
| ||
| 2(M+m)f |
答:(1)子弹射入并穿出木块的过程中木块在水平面上滑行的距离为
| m2(v0-v1)2 |
| 2Mf |
(2)要使子弹恰好不穿出,木块的长度应为
M
| ||
| 2(M+m)f |
点评:动能定理的应用不涉及运动过程的加速度、时间,一般比牛顿第二定律结合运动学公式解题要简便.在同一题中可以选择对不同研究对象运用动能定理去求解速度.要能知道运动过程中能量的转化,能用能量守恒定律的观点解决问题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目