题目内容
20. 如图所示,质量为M=2Kg的薄壁细圆管竖直放置,圆管内壁光滑,圆半径比细管的内径大的多,已知圆的半径R=0.4m,一质量为 m=0.5Kg的小球在管内最低点A的速度大小为2$\sqrt{3}$m/s,g取10m/s2,则下列说法正确的是( )
如图所示,质量为M=2Kg的薄壁细圆管竖直放置,圆管内壁光滑,圆半径比细管的内径大的多,已知圆的半径R=0.4m,一质量为 m=0.5Kg的小球在管内最低点A的速度大小为2$\sqrt{3}$m/s,g取10m/s2,则下列说法正确的是( )| A. | 小球恰好能通过最高点 | B. | 小球上升的最大高度为0.3m | ||
| C. | 圆管对地的最大压力为20N | D. | 圆管对地的最大压力为40N |
分析 小球运动过程中,只有重力做功,机械能守恒,根据机械能守恒定律求出小球沿圆轨道上升的最大高度,判断能不能上升到最高点,在最低点时,球对圆管的压力最大,此时圆管对地的压力最大,根据向心力公式和平衡条件列式求解.
解答 解:A、小球运动过程中,只有重力做功,机械能守恒,根据机械能守恒定律得:
$\frac{1}{2}$mv2=mgh
解得:h=$\frac{{v}^{2}}{2g}=\frac{(2\sqrt{3})^{2}}{20}$=0.6m<0.8m,不能上升到最高点,故A、B错误;
CD、在最低点时,球对圆管的压力最大,此时圆管对地的压力最大,根据向心力公式得:
N-mg=m$\frac{{v}^{2}}{R}$
解得:N=5+0.5×$\frac{{(2\sqrt{3})}^{2}}{0.4}$=20N,
根据牛顿第三定律得:球对圆管的压力为N′=N=20N
则圆管对地的最大压力为:FN=N+Mg=20+20=40N,故C错误,D正确.
故选:D
点评 本题主要考查了机械能守恒定律和向心力公式公式的直接应用,知道在最低点时,球对圆管的压力最大,此时圆管对地的压力最大.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
11.摆长为L的单摆,周期为T,若将它的摆长增加2m,周期变为2T,则L等于( )
| A. | $\frac{1}{3}$m | B. | $\frac{1}{2}$m | C. | $\frac{2}{3}$m | D. | 2m |
8.一束红光从空气射入折射率为1.5的玻璃,则这束红光的能量将( )
| A. | 增大 | B. | 减小 | C. | 不变 | D. | 无法确定 |
5. 如图甲是α、β、γ三种射线穿透能力的示意图,图乙是工业上利用射线的穿透性来检查金属内部伤痕的示意图,请问图乙中的检查利用的是( )
如图甲是α、β、γ三种射线穿透能力的示意图,图乙是工业上利用射线的穿透性来检查金属内部伤痕的示意图,请问图乙中的检查利用的是( )
 如图甲是α、β、γ三种射线穿透能力的示意图,图乙是工业上利用射线的穿透性来检查金属内部伤痕的示意图,请问图乙中的检查利用的是( )
如图甲是α、β、γ三种射线穿透能力的示意图,图乙是工业上利用射线的穿透性来检查金属内部伤痕的示意图,请问图乙中的检查利用的是( )| A. | α射线 | B. | β射线 | C. | γ射线 | D. | 三种射线都可以 |
9.电场强度的定义是E=$\frac{F}{q}$,点电荷场强的公式是E=$\frac{kq}{{r}^{2}}$,对这两个公式的理解正确的是( )
| A. | E=$\frac{F}{q}$中的场强E与电荷q无关,q 称为试探电荷 | |
| B. | E=$\frac{kq}{{r}^{2}}$中的场强E与电荷q有关,q称为场源电荷 | |
| C. | E=$\frac{F}{q}$中的F表示试探电荷受到的力 | |
| D. | E=$\frac{F}{q}$和E=$\frac{kq}{{r}^{2}}$都只对点电荷产生的电场才成立 |
10.下列说法中正确的有( )
| A. | 卢瑟福的a粒子散射实验揭示了原子核有复杂的结构 | |
| B. | 根据爱因斯坦质能方程,物体具有的能量和它的质量之间存在着正比关系 | |
| C. | 中子与质子结合成氘核的过程中需要吸收能量 | |
| D. | β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 |
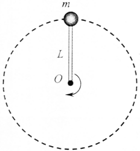 轻杆长L=60cm,一端固定于转轴O,另一端系一质量为m=0.5kg的小球,使小球在竖直平面内做圆周运动,重力加速度g=10m/s2,求:
轻杆长L=60cm,一端固定于转轴O,另一端系一质量为m=0.5kg的小球,使小球在竖直平面内做圆周运动,重力加速度g=10m/s2,求: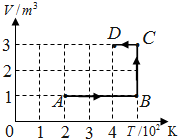 一定质量的某种理想气体由状态A变为状态D,其有关数据如图所示.若状态D的压强为104Pa,状态A的压强是多少?
一定质量的某种理想气体由状态A变为状态D,其有关数据如图所示.若状态D的压强为104Pa,状态A的压强是多少? 质量为m的带正电小球,电荷量为q,通过一根长为L的细线系于点O上.把细线拉直,让小球从P点由静止释放,OP连线与竖直方向的夹角为α=60°.由于水平方向电场的存在,使得小球到达竖直位置A时,速度恰好等于0.求:
质量为m的带正电小球,电荷量为q,通过一根长为L的细线系于点O上.把细线拉直,让小球从P点由静止释放,OP连线与竖直方向的夹角为α=60°.由于水平方向电场的存在,使得小球到达竖直位置A时,速度恰好等于0.求: