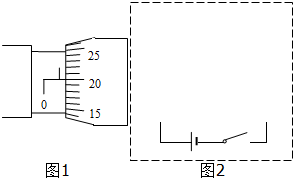
题目内容
4.某同学利用如图1所示的验证牛顿第二定律的实验装置来验证动能定理.实验时保持小车的质量不变,不断改变钩码的个数,用打点计时器和小车后端拖动的纸带测出小车运动的速度,绳中的拉力由拉力传感器读出.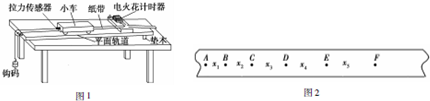
(1)实验时先不挂钩码,反复调整垫木的左右位置,直到小车能沿平面轨道做匀速直线运动,这一步骤叫平衡摩擦力.这样做的目的是实验中小车受到的合力等于拉力传感器的读数.
(2)该实验是否需要满足钩码的总质量远小于小车和拉力传感器的总质量?否.(填“是”或“否”)
(3)图2为实验中打出一条纸带的一部分,从比较清晰的点迹起,在纸带上标出了连续的6个计数点A、B、C、D、E、F,相邻两个计数点之间都有4个点迹没有标出,测出各相邻两个计数点间的距离分别为x1、x2、x3、x4、x5,已知打点计时器接在频率为f的交流电源两端,实验中从拉力传感器中读出小车受到的拉力为F,小车和传感器的总质量为M,钩码的质量为m,选取纸带上打B点到打E点的过程,写出验证动能定理的表达式F(x1+x2+x3+x4)=$\frac{1}{2}$Mf2($\frac{{x}_{4}+{x}_{5}}{10}$)2-$\frac{1}{2}$Mf2($\frac{{x}_{1}+{x}_{2}}{10}$)2.
分析 (1)明确平衡摩擦力的方法及意义即可回答:
(2)根据实验原理可分析是否需要使钩码的总质量远小于小车和传感器的质量;
(3)根据功的公式表示拉力的功;再根据平均速度公式求出速度,得出动能的表达式,则可验证动能定理.
解答 解:(1)垫起平面轨道的右端,让小车重力沿斜面向下的分力与它受到的摩擦力平衡,才能认为在实验中小车受到的合力等于拉力传感器的读数;
(2)由于在实验前已平衡摩擦力,故拉力传感器的读数就等于小车受到的合外力,故不需要使钩码的总质量远小于小车和传感器的质量;
(3)在打B点到E点的过程中,合力做功W=Fs=F(x1+x2+x3+x4);打B点时小车的速度为vB=$\frac{{x}_{1}+{x}_{2}}{10T}$=$\frac{f({x}_{1}+{x}_{2})}{10}$;同理可得,E点的速度为vE=$\frac{f({x}_{4}^{\;}+{x}_{5})}{10}$;则动能的变化量为:$\frac{1}{2}$mvE2-$\frac{1}{2}$mvB2;故验证动能定理的表达式为:
F(x1+x2+x3+x4)=$\frac{1}{2}$Mf2($\frac{{x}_{4}+{x}_{5}}{10}$)2-$\frac{1}{2}$Mf2($\frac{{x}_{1}+{x}_{2}}{10}$)2
故答案为:(1)使小车受到的合力等于拉力传感器的读数;(2)否;(3)F(x1+x2+x3+x4)=$\frac{1}{2}$Mf2($\frac{{x}_{4}+{x}_{5}}{10}$)2-$\frac{1}{2}$Mf2($\frac{{x}_{1}+{x}_{2}}{10}$)2
点评 本题考查验证动能定理的实验,要注意明确实验原理,根据原理得出需要做的步骤,并明确实验数据处理的方法.

 阅读快车系列答案
阅读快车系列答案
| A. | 电梯对货箱做的功等于货箱动能的增量 | |
| B. | 电梯对货箱做的功等于货箱增加的机械能 | |
| C. | 货箱处于超重状态 | |
| D. | 货箱处于失重状态 |
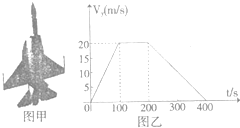 为了应对最新国际局势的变化,巴基斯坦高调举行“高标-2010”军演,在2010年8月6日达到高潮,巴基斯坦空军进行了导弹、炸弹以及其它实弹火力打击演练,证明了其为地面部队提供空中掩护的能力、图甲是中巴联合研制的“枭龙战机”,图乙是战机在演习中一次竖直向上拉起的速度-时间图象,则竖直拉起的过程中关于战机运动的说法正确的是( )
为了应对最新国际局势的变化,巴基斯坦高调举行“高标-2010”军演,在2010年8月6日达到高潮,巴基斯坦空军进行了导弹、炸弹以及其它实弹火力打击演练,证明了其为地面部队提供空中掩护的能力、图甲是中巴联合研制的“枭龙战机”,图乙是战机在演习中一次竖直向上拉起的速度-时间图象,则竖直拉起的过程中关于战机运动的说法正确的是( )| A. | 飞机在前100s内竖直方向加速度大小为0.2m/s2 | |
| B. | 400s末飞机回到出发点 | |
| C. | 200s末飞机开始返回,加速度大小为0.1m/s2 | |
| D. | 这次飞行中飞机上升达到最大高度为5000m |
 在倾角为θ的固定光滑斜面上有两个轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则( )
在倾角为θ的固定光滑斜面上有两个轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d,速度为v,则( )| A. | 物块A的重力势能增加m1gd | |
| B. | 物块B的质量满足m2gsinθ=kd | |
| C. | 此时物块A的加速度为$\frac{F-{m}_{1}gsinθ-kd}{{m}_{2}}$ | |
| D. | 此过程中,弹簧的弹性势能变化了Fd-m1gdsinθ-$\frac{1}{2}$m1v2 |
| A. | 估算金属原子的大小时可以把原子看成是球形或立方体 | |
| B. | 物体由大量分子组成,其单个分子的运动是无规则的,大量分子的运动也是无规律的 | |
| C. | 分子间的相互作用随着分子间距离的增大,一定先减小后增大 | |
| D. | 在各种晶体中,原子(或分子、离子)都是按照一定的规律排列的,具有空间上的周期性 | |
| E. | 任何热机都不可能使燃料释放的热量完全转化为机械能 |
 如图所示,光滑的斜面上垂直纸面放置一根直导体棒,欲使导体棒中的电流垂直纸面向里时导体棒能静止在斜面上,下列外加匀强磁场的方向可能正确的是( )
如图所示,光滑的斜面上垂直纸面放置一根直导体棒,欲使导体棒中的电流垂直纸面向里时导体棒能静止在斜面上,下列外加匀强磁场的方向可能正确的是( )| A. | 水平向右 | B. | 水平向左 | C. | 平行斜面向上 | D. | 垂直斜面向下 |
 如图所示,在坐标系xOy的第一象限内斜线OC的上方存在垂直纸面向里的匀强磁场,磁感应强度为B,第四象限内存在磁感应强度大小未知,方向垂直纸面向里的匀强磁场,第三象限内存在沿y轴负方向的匀强电场,在x轴负半轴上有一接收屏GD,GD=20D=d,现有一带电粒子(不计重力)从y轴上的A点,以初速度v0水平向右垂直射入匀强磁场,恰好垂直OC射出,并从x轴上的P点(未画出)进入第四象限内的匀强磁场,粒子经磁场偏转后又垂直y轴进入匀强电场并被接收屏接收,已知OC与x轴的夹角为37°,OA=$\frac{4}{5}$d,求:
如图所示,在坐标系xOy的第一象限内斜线OC的上方存在垂直纸面向里的匀强磁场,磁感应强度为B,第四象限内存在磁感应强度大小未知,方向垂直纸面向里的匀强磁场,第三象限内存在沿y轴负方向的匀强电场,在x轴负半轴上有一接收屏GD,GD=20D=d,现有一带电粒子(不计重力)从y轴上的A点,以初速度v0水平向右垂直射入匀强磁场,恰好垂直OC射出,并从x轴上的P点(未画出)进入第四象限内的匀强磁场,粒子经磁场偏转后又垂直y轴进入匀强电场并被接收屏接收,已知OC与x轴的夹角为37°,OA=$\frac{4}{5}$d,求: