��Ŀ����
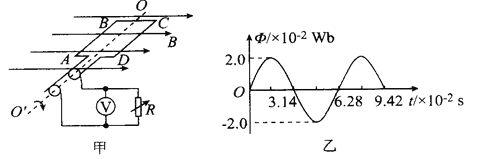
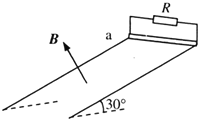
����Ŀ������ɺ��ԵĹ⻬ƽ�н������쳤S=1.3m����������![]() m���������Ϊ30�㣬�����϶�ab��һ��ֵR=1.5���ĵ��裬�Ÿ�Ӧǿ��B=0.8T����ǿ�ų���ֱ���ƽ������.��ֵr=0.5��������m=0.2�K�Ľ�����������ֱ�ҽӴ����ã��ӹ���϶�ab���ɾ�ֹ��ʼ�»�������б��Ͷ˵��ٶ�Ϊv=3m/s��ȡg=10m/s����
m���������Ϊ30�㣬�����϶�ab��һ��ֵR=1.5���ĵ��裬�Ÿ�Ӧǿ��B=0.8T����ǿ�ų���ֱ���ƽ������.��ֵr=0.5��������m=0.2�K�Ľ�����������ֱ�ҽӴ����ã��ӹ���϶�ab���ɾ�ֹ��ʼ�»�������б��Ͷ˵��ٶ�Ϊv=3m/s��ȡg=10m/s����
(1)�������»���б��Ͷ�ʱ�ļ��ٶ�.
(2)�������»���б��Ͷ˵Ĺ����е���R�ϲ����Ľ�����.
���𰸡�(1) 2.3m/s��(2) 0.3J��
�������������������1������������������������������ܵ�������֧������������������ţ�ٵڶ�������ü��ٶȣ���2�����ݶ��ܶ����ͽ�����������������R�ϲ����Ľ����ȣ�
��1���������»��ٶ�![]() ʱ�����ܵİ�����Ϊ��
ʱ�����ܵİ�����Ϊ�� 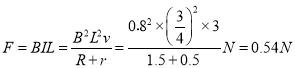
��ţ�ٵڶ����ɵã� ![]()
��ã� ![]()
��2�����ݶ��ܶ����ɵã� ![]()
���ݹ��ܹ�ϵ�ɵò�����������![]()
��ã�Q=0.4J
�����R�ϵĽ�����Ϊ�� ![]()

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ