题目内容
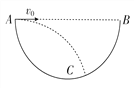
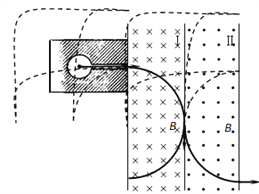
【题目】在一个放射源水平放出![]() 三种射线,垂直射入如图所示磁场,区域I和II的宽度均为d,各自存在着垂直纸面的匀强磁场,两区域的磁感应强度大小B相等,方向相反(粒子运动不考虑相对论效应)。
三种射线,垂直射入如图所示磁场,区域I和II的宽度均为d,各自存在着垂直纸面的匀强磁场,两区域的磁感应强度大小B相等,方向相反(粒子运动不考虑相对论效应)。
(1)若要筛选处速率大小![]() 的所有
的所有![]() 粒子进入区域II,求磁场宽度d与B和
粒子进入区域II,求磁场宽度d与B和![]() 的关系;
的关系;
(2)若B=0.0273T, ![]() (c是光速度),计算d;
(c是光速度),计算d; ![]() 粒子的速率为0.001c,计算
粒子的速率为0.001c,计算![]() 粒子和
粒子和![]() 射线离开区域I时的距离(答案均保留三位有效数字);
射线离开区域I时的距离(答案均保留三位有效数字);
(3)当d满足第(1)小题所给关系时,请给出速率在![]() 区间的β粒子离开区域II时的位置。已知电子质量me=9.1×10-31kg,α粒子质量mα=6.7×10-27kg,电子电荷量q=1.6×10-19C,
区间的β粒子离开区域II时的位置。已知电子质量me=9.1×10-31kg,α粒子质量mα=6.7×10-27kg,电子电荷量q=1.6×10-19C, ![]() (
(![]() 时)
时)

【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】(1)作出临界轨道,由几何关系知r=d,由![]() 得
得![]()
(2)对电子: ![]()
对![]() 粒子:
粒子: ![]()
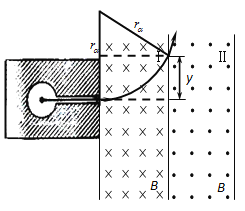
作出轨道如图,竖直方向上的距离
![]()
(3)画出速率分别为v1和v2的粒子离开区域Ⅱ的轨迹如下图
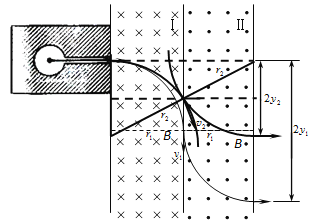
速率在 v1<v<v2区域间射出的β粒子束宽为(2y1-2y2)
![]()
![]()
点睛; 本题考查带电粒子在磁场中的运动,本知识点由于结合较多的数学知识,特别是圆的性质,故此类题型重点在于熟练把握圆的性质;可以先大致画出圆的轨迹,根据偏转方向等确定出圆心和半径,再利用几何知识求出结果.

练习册系列答案
相关题目