题目内容
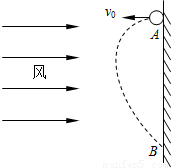
如图所示，在足够高的竖直墙面上A点，以水平速度v0向左抛出一个质量为m的小球，小球抛出后始终受到水平向右的恒定风力的作用，风力大小为F，经过一段时间小球将再次到达墙面上的B点处，重力加速度为g，则在此过程中：
（1）小球在水平方向和竖直方向各作何种运动？
（2）小球水平方向的速度为零时距墙面的距离？
（3）墙面上A、B两点间的距离？
（4）小球的最大速率vmax？
（5）小球的最小速率vmin？
（1）小球在水平方向和竖直方向各作何种运动？
（2）小球水平方向的速度为零时距墙面的距离？
（3）墙面上A、B两点间的距离？
（4）小球的最大速率vmax？
（5）小球的最小速率vmin？
（1）小球在水平方向先向左做匀减速运动而后向右做匀加速运动，小球在竖直方向上做自由落体运动．
（2）将小球的运动沿水平方向和竖直方向分解
水平方向：F=max，得ax=
则x=
=
．
（3）水平方向速度减小为零所需的时间t1=
所以t=2t1=
=
．
竖直方向上：y=
gt2=
．
（4）小球运动到B点的速度最大．
vx=v0
vy=gt=
vmax=
=
．
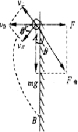
（5）将运动沿图示方向分解．
当v⊥=0时，小球速度最小．
此时vmin=v∥=v0cosθ
根据力的关系知cosθ=
．
解得vmin=
．
答：（1）小球在水平方向先向左做匀减速运动而后向右做匀加速运动，小球在竖直方向上做自由落体运动．
（2）小球水平方向的速度为零时距墙面的距离为
．
（3）墙面上A、B两点间的距离为
．
（4）小球的最大速率为vmax=
．
（5）小球的最小速率为vmin=
．
（2）将小球的运动沿水平方向和竖直方向分解
水平方向：F=max，得ax=
| F |
| m |
则x=
| v02 |
| 2ax |
| mv02 |
| 2F |
（3）水平方向速度减小为零所需的时间t1=
| v0 |
| ax |
所以t=2t1=
| 2v0 |
| ax |
| 2mv0 |
| F |
竖直方向上：y=
| 1 |
| 2 |
| 2m2gv02 |
| F2 |
（4）小球运动到B点的速度最大．
vx=v0
vy=gt=
| 2mgv0 |
| F |
vmax=
| vx2+vy2 |
| v0 |
| F |
| F2+4m2g2 |
（5）将运动沿图示方向分解．
当v⊥=0时，小球速度最小．
此时vmin=v∥=v0cosθ
根据力的关系知cosθ=
| mg | ||
|
解得vmin=
| mgv0 | ||
|
答：（1）小球在水平方向先向左做匀减速运动而后向右做匀加速运动，小球在竖直方向上做自由落体运动．
（2）小球水平方向的速度为零时距墙面的距离为
| mv02 |
| 2F |
（3）墙面上A、B两点间的距离为
| 2m2gv02 |
| F2 |
（4）小球的最大速率为vmax=
| v0 |
| F |
| F2+4m2g2 |
（5）小球的最小速率为vmin=
| mgv0 | ||
|
练习册系列答案
阅读快车系列答案
相关题目
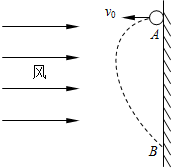如图所示，在足够高的竖直墙面上A点，以水平速度v0向左抛出一个质量为m的小球，小球抛出后始终受到水平向右的恒定风力的作用，风力大小为F，经过一段时间小球将再次到达墙面上的B点处，重力加速度为g，则在此过程中：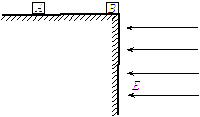
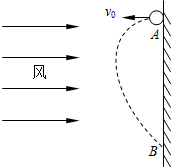如图所示，在足够高的竖直墙面上A点，以水平速度v0向左抛出一个质量为m的小球，小球抛出后始终受到水平向右的恒定风力的作用，风力大小为F，经过一段时间小球将再次到达墙面上的B点处，重力加速度为g，则在此过程中：